みなさん、こんにちは。
受験Dr.の坂井です。
今回は、角度の問題についてのお話です。
正多角形に対角線が引いてあり、辺や対角線どうしで作る角度を求める問題を瞬間的に解いてしまおうというお話になります。
結論からいうと、正ｎ角形において、辺や対角線で作ることができる角度の大きさは、
の大きさになります。これを利用して角度を求めてみましょう。
正八角形を例に、辺や対角線でどのような角度が作られるかを下の図で見ていきましょう。
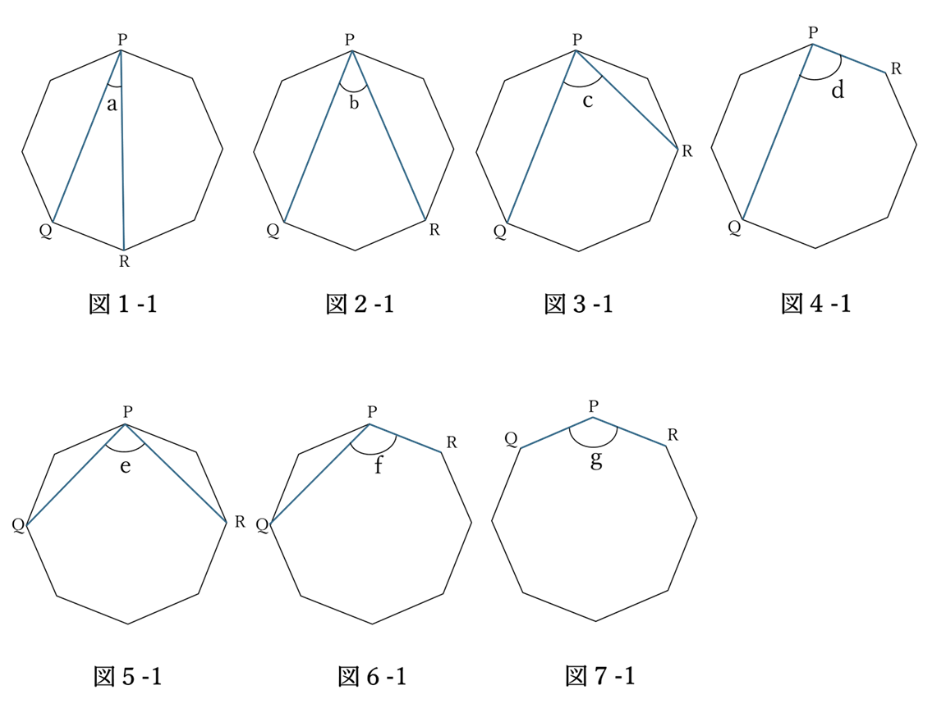
図１-１〜図７-１は、正八角形の辺や対角線で作ることができる角度を示しています。
そして、その辺や対角線を平行移動させたときの様子を、図１-2〜図7-２で見てみます。
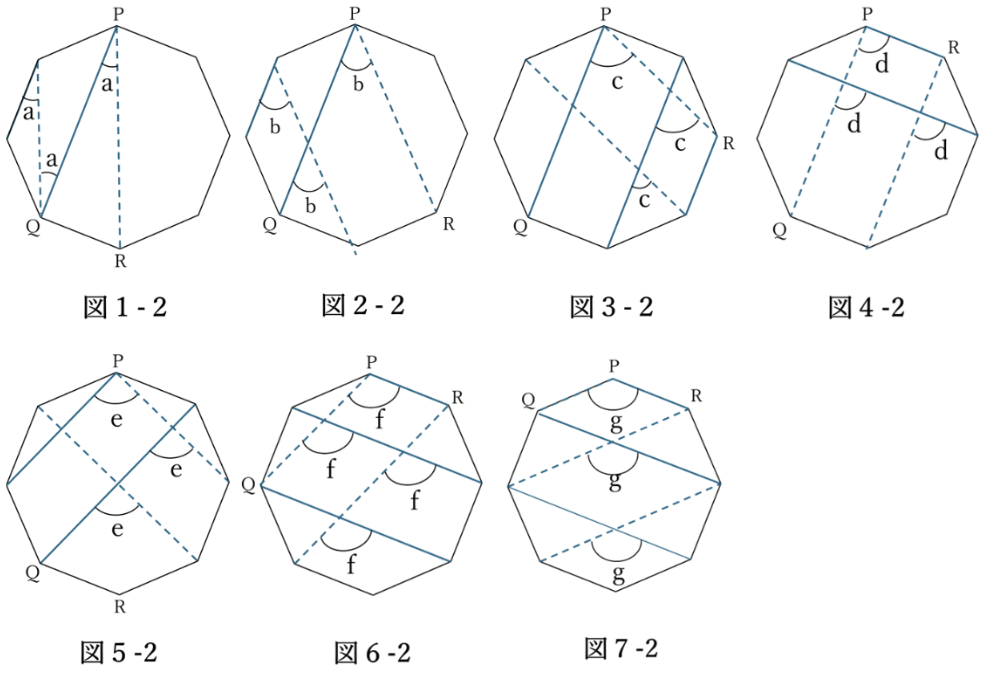
角a〜角ｇが正八角形の辺や対角線で作ることができる角の大きさになっていることがわかります。
ここで、角a〜角ｇの大きさを求めてみましょう。
角a
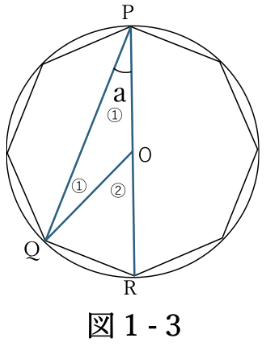
図１-３のようにOP＝OQだから角OPQ＝角OQP＝①
外角の定理より、角QOR＝360÷８＝45°
よって角a＝45÷2＝22.5° となります。
これは
となり、
n=8のときのになります。
つまり、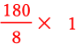
となります。
角ｂ
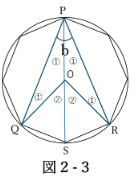
角ｂ＝角QPO×２だから、22.5×２＝45° となる。
また、角QOR＝360/8×2
角ｂ＝角QOR×1/2（円周角の定理）と考えてもよい。
これもとなり、
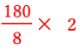になります。
角ｃ
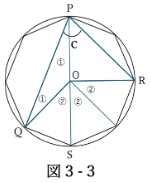
角QOR=360/8×3＝135°
角ｃ＝角QOR×1/2＝67.5°（円周角の定理）
これもとなり、
になります。
角ｄ
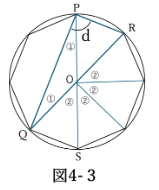
角QOR=360/8×4＝180°
角ｄ＝角QOR×1/2＝90°（円周角の定理）
これもとなり、
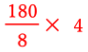になります。
角e
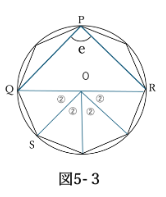
角QOR=360/8×4＝180°
角e＝角QOR×1/2＝90° （円周角の定理）
これもとなり、
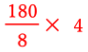になります。
角ｆ
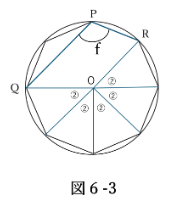
角QOR=360/8×5＝225°
角ｆ＝角QOR×1/2＝112.5° （円周角の定理）
これもとなり、
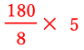
になります。
角ｇ
角QOR=360/8×6＝270°
角g＝角QOR×1/2＝135° （円周角の定理）
これもとなり、
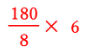になります。
以上より、角a～角gはいずれも
となります。
正八角形の辺や対角線で作る角度の大きさは、
22.5°，45°，67.5°，90°，112.5°，135°のいずれかになることがわかります。
あとは、どの大きさに近いのだろうかと見た目で判断し、解答していくことになります。
こんな風に考えていきます。
【問題】
下の図で、∠ア，∠イの大きさを求めなさい。
∠アは、明らかに見た目で45°より大きいです。そして90°までは大きくない。
よって、67.5°となります。
∠イは、22.5°よりは明らかに大きく、正三角形の１つの内角である60°より小さいので45°となります。
では、練習問題してみましょう。ぜひ、チャレンジしてみてください。
下の図は、正五角形、正六角形、正八角形、正十角形です。
㋐〜㋖の角の大きさをそれぞれ求めなさい。
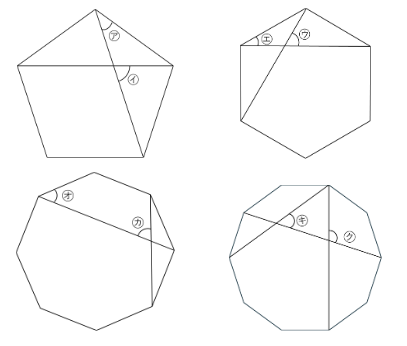
答え ㋐36° ㋑72° ㋒30° ㋓60° ㋔45° ㋕67.5° ㋖54° ㋗108°
どうでしたか。決して積極的に利用してほしい解法ではありませんが、通常通り１つずつ角の大きさを求めてたどり着いた答えが、これらの候補（22.5の倍数）と違っていたら計算し直してみるといった「間違え防止機能」としては十分に役立つのではないでしょうか。
まとめ
①正ｎ角形において、辺や対角線で作ることができる角度の大きさは、
②積極的に利用する解法ではないが、「間違え防止機能」としては効果的。
というものでした。
それでは、みなさん
またお会いしましょう。
