こんにちは。算数を担当しています佐々木裕子です。

本日は、速さの問題を解く上で、進行グラフと進行図どちらを使った方がいいのかということについて分析していきたいと思います。

1つの問題を使って両方の解き方を示していきます。

【愛光中　2016年より】
太郎君と次郎君はそれぞれ自転車でA地点を出発し、B地点を通りC地点まで行きます。太郎君は7時にA地点を出発し、7時24分にB地点を通り、B地点からは速さを1分あたり20m遅くしたので、7時49分にC地点に到着しました。次郎君は7時10分にA地点を出発し、B地点を通り、B地点から速さを遅くしたので、7時46分にC地点に到着しました。A地点からB地点までとB地点からC地点までの距離の比が16：15、次郎君のA地点からB地点までとB地点からC地点までの速さの比が4：3のとき、次の問いに答えなさい。
(1)太郎君のA地点からB地点までの自転車の速さは分速何mですか。
(2)次郎君のA地点からB地点までの自転車の速さは分速何mですか。
(3)次郎君が太郎君に追いついたのはA地点から何mのところですか。

まず、進行グラフを描いてみると

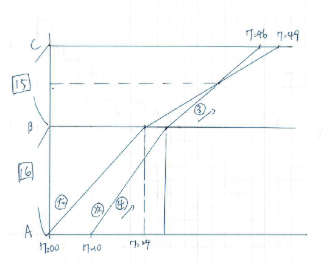
いかがでしょうか。
進行グラフは、文章を読んだときに、どこで追いついたか、太郎君の方が次郎君より速いのか遅いのかが分からないので、進行グラフを描くときに、「ここで抜くだろう」と予想しながら
書く必要があります。メリットとしては、時間と場所が分かりやすく、見つけやすいのですが、
デメリットは、書くときに分析しながら書き進める力が必要になります。

では、進行図はどうでしょうか。

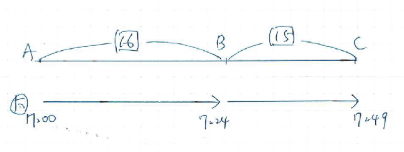
こちらの方が描く情報や線が進行グラフより少ないようです。
進行図は、「同じ距離」や「同じ時間」「同じ速さ」というように、比を利用することを
前提として書かれているので、シンプルで見つけやすいということがあります。
ただ、同じ時間を表すときは、「同じ時刻マーク」（▲など「同じ時間にここにいた」を表すマーク）をつけて比べる必要があります。

結論は、どちらでもいいと思います。自分が書き慣れたもので解き進める方がいいですし、実際この問題も進行グラフで解く生徒さんもいます。

進行グラフと進行図はそれぞれ向き不向きがあります。
進行グラフを利用するのは、
①行ったり来たりして止まる(バスの往復で駅で止まる)
②時間がずれて出発し往復、途中で戻る
などの場合でしょうか。グラフを描くと、平行線と斜めの線に当たるグラフで相似形や高さが等しい三角形の利用ができるというメリットがあります。

進行図のメリットは、
①シンプルである
②比が見つけやすい（比べるところが見つけやすい）
というのが挙げられます。

時間が同時ではない時は、同時刻マークを付ければいいので、問題を解く上では、原則、進行図を勧めます。ただ、行ったり来たりして止まったり速さを変えてしまう場合は、進行グラフの方がよいでしょう。

ちなみに、この愛光中の問題を解くと、

（1）　1624：1525＝20：18＝10：9
⑩－⑨＝①＝20m/分
⑩＝20×10＝200m/分

(2)　次郎君は、A～B、B～Cにそれぞれ
16÷④：15÷③＝4：5の時間かかっているので、
トータル7：46―7：10＝36分
36分÷（④＋⑤）＝4分　　4分×④＝16分
AからBまでの距離は、200×24＝4800m
4800m÷16＝300m/分

(3)　次郎君は、B～Cは、300÷④×③＝225m/分
太郎君は、B～Cは、200―20＝180m/分
B地点に次郎君がついたとき、7時26分なので、太郎君より2分遅れている
2分で太郎君は、2×180＝360m前にいるので、それを追いかけます。
360÷(225―180)＝8分　225×8分＝1800m
よって、1800m＋4800m＝6600m地点で追いつくことになります。