こんにちは。算数を担当しています佐々木裕子です。

本日は、桜蔭2021年度(令和3年)の問題です。

【桜蔭　2021年　大問Ⅳより】
円周率は、3.14を使って計算することが多いです。しかし、本当は3.14159265…とどこまでも続いて終わりのない数です。この問題では、円周率を3.1として計算してください。
図のように点Oを中心とした半径の異なる2つの円の周上に道があります。Aさんは内側の道を地点aから反時計回りに、Bさんは外側の道を地点bから時計回りに、どちらも分速50mの速さで同時に進み始めます。AさんとBさんのいる位置を結ぶ直線が点Oを通るときに、ベルが鳴ります。ただし、出発のときはベルは鳴りません。

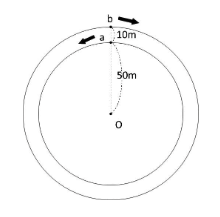
(1)　AさんとBさんが道を1周するのにかかる時間はそれぞれ何分ですか。
(2)　1回目と2回目にベルが鳴るのは、それぞれ出発してから何分後ですか。
(3)　出発してから何分かたったあと、2人とも歩く速さを分速70mに同時に変えたところ、5回目にベルが鳴るのは速さを変えなかったときと比べて1分早くなりました。速さを変えたのは、出発してから何分後ですか。

（1）と（2）の解説は省略いたします。
本日は（3）について、考えていきたいと思います。

角速度を利用して解いていきます。
(1)より、Aが1周するのにかかる時間は、6.2分、
Bが1周するのにかかる時間は、7.44分となるので、
それぞれの角速度は、A＝360°÷6.2分＝１８００３１°

Bは360°÷7.44分＝１５００３１°

はじめの速さのまま進むと(2)より、９３５５分ごとにベルが鳴るので、5回目になるのは、
９３５５×5＝９３１１分後です。

速さを変える前と後の角速度の比は、2人とも50：70ですから、
かかる時間の比は7：5

速さを変える前までを□分とすると、速さを変えた後に差の1分が生じるので、
⑦－⑤＝②が1分に当たることになります。

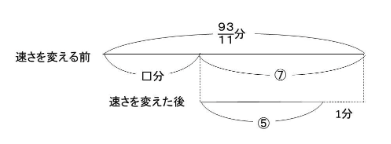
②＝1分
①＝0.5分
⑦＝3.5分
□＝９３１１―3.5分＝１０９２２＝4２１２２分
となります。

⑦＝3.5分

他に、シャドーを利用して解く方法もありますが、角速度にした方が、
式は楽に解けると思います。
一度、シャドーを利用して解いてみるのもいいかもしれません。

次回もお楽しみに！