みなさん、こんにちは。受験Dr.の亀井章三です。

今回は「難問を解く方法」です。
解くのが難しい問題は、どこに着目しどう展開していくのか。
2025年筑波大附属駒場中学の入試問題を使用して説明します。

筑駒の算数は大問4題で、小問が3～4問となっています。
試験時間が40分と短いためテンポよく解いていく必要があります。

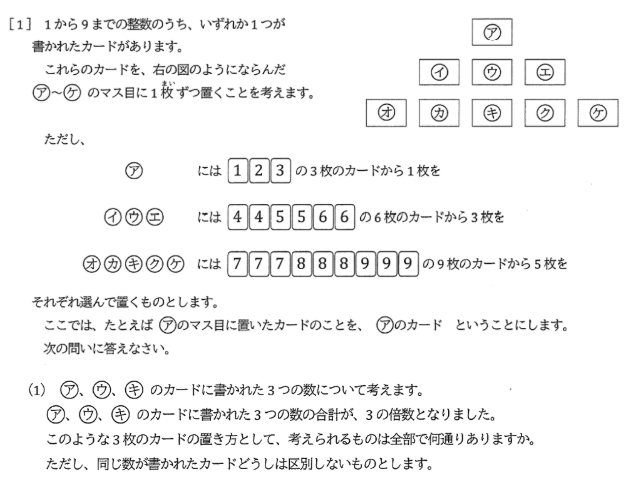
場合の数は、まず「全部調べるとしたら何通り」かを考えましょう。
ア、ウ、キ全て３通りずつあるので、3✕3✕3＝27通りです。
これはそんなに多くありませんので、樹形図を描いて答えを求めましょう。
(1,4,7)(1,5,9)(1,6,8)(2,4,9)(2,5,8)(2,6,7)(3,4,8)(3,5,7)(3,6,9)の9通りです。

(1)から繋がる問題です。先にこちらの問題を見ていたら、(1)で9通り全て
書き出すことが必要だとわかるでしょう。
イ、ウ、エに並べる3枚の組み合わせを考えると(4,5,6)しかありません。
ア、ウ、キとイ、ウ、エの両方に共通するのはウなので、ウに入る数から考えます。
ウ＝4のとき、アとキに入るカードの組み合わせは3通り、イとエに入るカードの
組み合わせは2通りなので、3✕2＝6通りです。
ウ＝５、ウ＝６のときも同様なので、6✕3＝18通りです。

これも(2)から繋がる問題です。ア、イ、ウ、エ、キの組み合わせと、
オ、カ、キ、ク、ケの組み合わせの積を求めることになります。
オ、カ、キ、ク、ケの組み合わせですが、9枚から5枚選ぶのではなく、
「選ばない4枚」を選ぶほうが求めやすいです。
細かく場合分けをする必要があるので、(1)(2)を最低限の時間だけで解き、
(3)にしっかり５～６分くらいかけて答えを求めましょう。

規則はしっかり書かれているので、「〇組の△番目」のように記録しながら
数字を確認しましょう。
まず上から8段目、左から8列目は③の真ん中＝3組の7番目
と分かります。3組は51から始まるので、51＋6＝57と求められます。

の逆パターンです。203は9組の3番目の数です。
図１・図２と照らし合わせながら答えを求めましょう。ここは時間をあまり
かけず正解を求めたいところです。

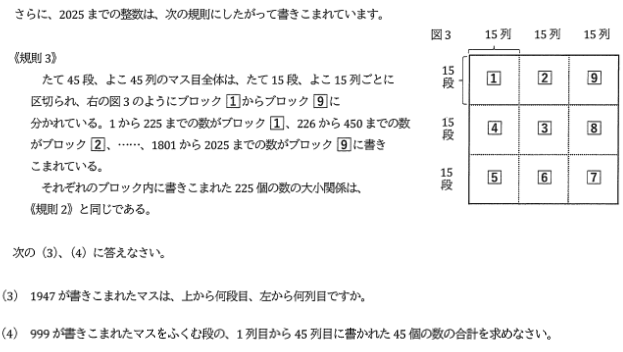
(1)(2)と同じように解いていけば良いのは分かります。ただ、数が大きいため
一つひとつ確認しながら解き進めましょう。
それでも(4)はかなり大変です。先に大問３、４に進むのが良いでしょう。
(3)は解きましょう。1947÷225＝8あまり147→ 9⃣の147番目
147÷25＝5あまり22→ 9⃣の中の6組22番目
＝ 9⃣の中の上から14段・右から10列
よって、上から14段、右から40列となります。

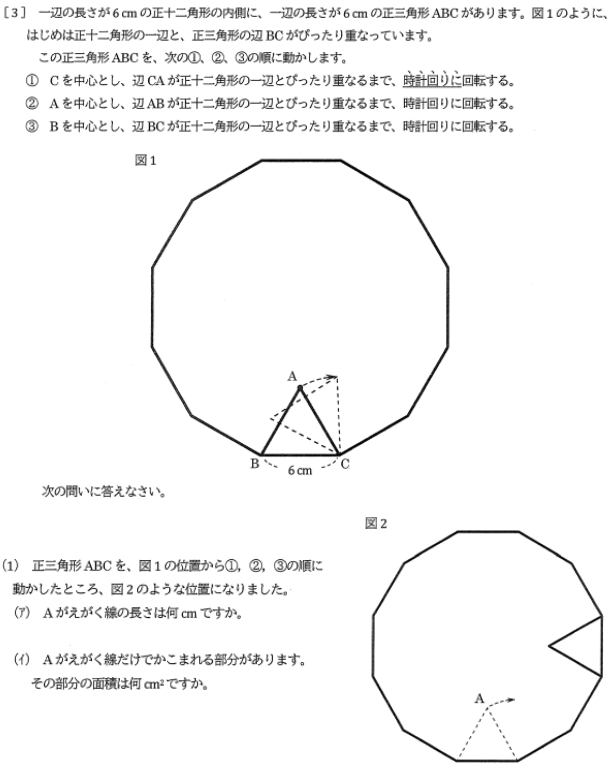
図形の問題は丁寧に作図しましょう。試験ではコンパスや定規が使えない場合が
多いので、ついフリーハンドで図を描くことだけしている人も多いと思います。
しかし、普段の学習ではコンパス・定規を用いて丁寧な図を描き、「正しい図の
イメージ」をおぼえましょう。特に(イ)のように囲まれる部分は、正確な図を描かない
と間違える可能性が高いです。

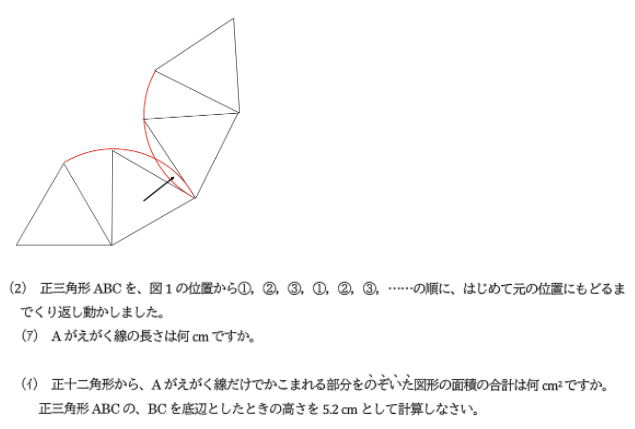
(ア)は(1)と同じ動きがくり返されるので、(1)(ア)の答えの4倍をすぐに
求めましょう。
(イ)は単純に4倍ではありません。中央付近にもう一つ軌跡で囲まれる
図形が現れることです。それらを正十二角形から引きます。
正三角形の面積に関する情報が与えられたときは、「正三角形を使う」
ということも意識しておきましょう。

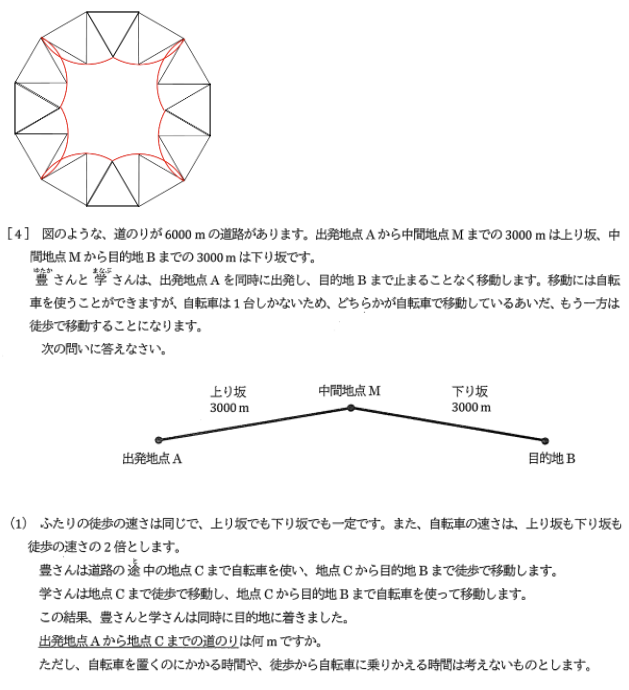
速さだから面倒だなぁと思うとダメです。速さが上りと下りで変わりませんので、
2人が同時に着くには、「歩いた距離と自転車の距離」が等しくないといけません。
（豊が自転車で進んだ距離＝学ぶが歩いた距離のため、等しくなければ自転車
で進んだ距離が長い人が早く着きます）
ということは、C=中間地点のMとなり、3000mと計算しなくても求められます。
筑駒の(1)はこういう難易度も問題も出ますので、見た目に惑わされないように
しましょう。

(ア)は上りと下りの速さが異なります。D地点が上り坂の途中か下り坂の途中かで
場合分けをし、式を作って考えましょう。
Dが上り坂の途中にある場合
徒歩の速さ：毎分1m、自転車の上りの速さ：毎分2m、下りの速さ：毎分4m
ADの距離を〇ｍとすると
豊さんは、〇÷２＋（3000－〇）÷１＋3000÷１＝6000－〇×1/2
学ぶさんは、〇÷１＋（3000－〇）÷２＋3000÷４＝2250＋〇×1/2
これが等しいので、〇＝3750となりますが、これはＤが上り坂の途中にある
という仮定に反するのでダメです。
Ｄが下り坂の途中にある場合、ＭＤの距離を〇ｍとすると
豊さんは、3000÷２＋〇÷４＋（3000－〇）÷１＝4500－〇×3/4
学ぶさんは、3000÷１＋〇÷１＋（3000－〇）÷４＝3750＋〇×3/4
〇×3/2＝750　〇＝500となり、条件に合います。よって3500ｍが答えです。
小学生らしくない解き方かもしれませんが、これが最速で効率の良い解法です
ので、身に付けておくと良いです。

(イ)も同様に式処理で解くことができます。言いかえれば、式処理だけで解ける
問題は練習している人であれば、ほぼ確実に正解できるため、「落とせない問題」
であるとも言えます。

今回は筑波大附属駒場中2025年の問題を用いて、難問を解くためのポイントを説明しました。筑駒の「難しい」ポイントは、解答時間の短さに対する処理量の多さと
言えるでしょう。普段の学習でも、「正解する」から「最速で正解する」への意識変化
が必須です。漫然と解かず、常にレベルアップを図っていきましょう。