皆さんこんにちは。
受験Dr.講師の勝山利信です。

今回は平面図形の問題をテーマに「状況に応じた裏技の活用」についてお話します。
何をもって「裏技」とするのかですが、ここでは①使用する機会が限定される解法であること、②根本的な理解は飛び越えて解法だけ覚えることを指しているとします。

解答を正しく早く求めることを目的とする

ここでは、中学受験の対策のために解答を正しく早く求めることを学習目標としてお話します。
学問として算数・数学を学ぶ場合と、優先するべきことが異なりますのでご注意ください。

それでは、次のような問題をどのように解いていくのか考えて見ましょう。
＜問題＞
次の図において、辺ABを2：3に分ける点をD、辺ACを1：2に分ける点をEとします。BEとCDが交わった点をFとし、AFを延長して辺BCと交わった点をGとします。このとき、AF：FGを求めなさい。

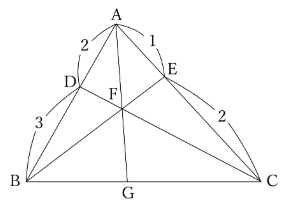
通称「ベンツ切り」や「ブーメラン型」と呼ばれる特徴的な配置の図ですね。

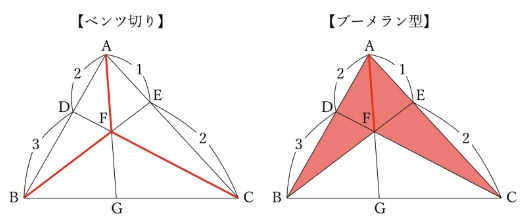
三角形ABF、ACF、BCFの面積比をとらえて辺の比を考えることが、本質的に辺の比と面積比の関係を理解して解く方法です。
しかし、中には細かく面の分割を考えると大きさの関係性が認識しきれなくなってしまう人もいるでしょう。
そのときに効果を発揮する裏技が「てんびんの利用」です！

辺をてんびんの棒ととらえ、てこの原理の仕組みから重さと長さのバランスを考えて見ます。

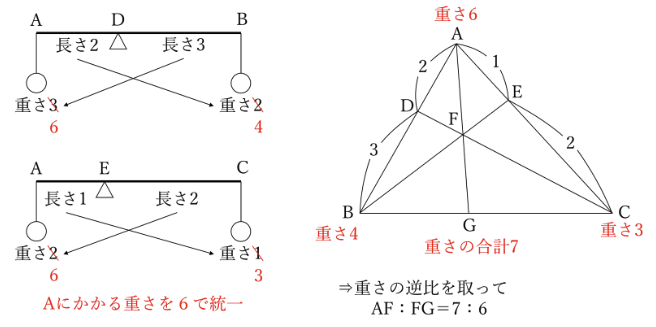
すると、面積がどのように分割されているかは分からなくても、正しい結論は求められます。

学習上の注意事項

この問題であれば、辺の比と面積の分割との関係を理解している上で、数値の処理は簡単に済ませられることが理想的です。ですが、中学受験のための対策と考えた場合は、正しい結論を出せることを一旦優先するということも良いことです。入試までの期限が限られているので、それまでに結果につなげるためだと考えましょう。

ただし、注意しなければならないのは、中学校以降の学習では同じような姿勢で学ばないということです。特に高校数学の内容においては、付け焼き刃的な方法では対処できなくなります。

中学受験の学習内容は中学校や高校の内容の前倒しであることも多いので、その期間を乗り越えるためには裏技を部分的に使うこともやむを得ないというのも選択肢の一つです。

状況に応じた使い分け

「理解してなくても解ければ良い」と聞くと少し乱暴に聞こえてしまうかもしれませんが、そもそも算数の学習では、円周率がなぜ約3.14なのか、円錐の体積はなぜ同じ底面積・高さの円柱の体積の3分の1なのか、理屈が分かっていないにも関わらず、事実としてとらえて使用するということは日頃からしています。

私も指導においては、生徒の状況や入試までの残り期間に応じてどのような解き方や考え方を身につけるべきか調整しています。「解ける！」という喜びが得られると次の学習にもつながりやすいので、算数のつまずきによってモチベーションが下がってしまっているときなどは参考にしてみてください。

それでは、またお会いしましょう！