みなさん、こんにちは。
受験Dr.算数科の江田です。

今回は「和差算」について。
“複数個ある数量の和と差がわかっているとき”にそれぞれの数量を求める問題、
それが「和差算」です。

この和差算、
「大小関係を表す線分図をかいて、いずれかに大きさ(長さ)をそろえる」
という流れで考えていきます。

さっそく実際にやってみましょう。

【例題１】
大小2つの整数があり、これらの差は35で、和は91です。
この2つの整数のうち、大きい方の数を求めなさい。

まずはこの大小2つの整数の大小関係を線分図で表します。

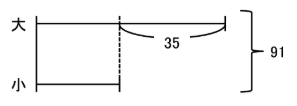
さて、ここから一方に大きさ(長さ)をそろえて考えます。
たとえば、「小」にそろえてみましょうか。

そのためには、「大」を35減らす(短くする)必要があり、
2つの整数の和も35減って
91－35＝56
となり、下の図のようになります。

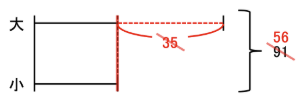
つまり、
「小2本ぶんの和が56」
とわかり、「小」が
56÷2＝28
と求められますね。
よって、「大」は
28＋35＝63　(または91－28＝63)
と求まります。

 

今は線分図を「小」にそろえて考えてみましたが、
「大」にそろえてみるとどうなるか考えてみましょう。

そのためには、「小」を35増やす(長くする)必要があり、
2つの整数の和も35増えて
91＋35＝126
となり、下の図のようになります。

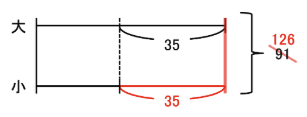
つまり、今度は
「大2本ぶんの和が126」
とわかり、「大」が
126÷2＝63
と求められますね。

 

どうでしょう。
お気づきになりましたか。

そう、和差算は
「そろった長さ(数値)が先に求まる」のです。

なので、
「大を求めたかったら大にそろえる」ことが
答えにたどり着くまでの最短ルートなのです。

ということで、
「和差算は求めたいものに線分図をそろえろ！」
これが今回伝えたいこと。
今回はこれを合言葉に問題に取り組みましょう！

それではもう1問。

【例題２】
大中小3つの整数があり、これら3つの和は238です。
また、大は中より17大きく、中は小より10大きくなっています。
中はいくつですか。

 

まずは、この大中小3つの整数の大小関係を線分図で表します。

さて、どれにそろえるべきか…

今回の合言葉
「和差算は求めたいものに線分図をそろえろ！」

ということで、「中」の長さにそろえるべきですね！
すると、
「大」は17小さく(短く)、「小」は10大きく(長く)する必要があり、
3つの整数の和は
238－17＋10＝231
となり、下の図のようになります。

つまり、
「中3本ぶんの和が231」
とわかり、「中」は
231÷3＝77
と求まりますね！

 

いかがでしたか。

現場で指導にあたっていると、和差算を解くときに
“常に一番短い線分図にそろえて解いている”
という受験生は少なくないと感じます。

「中」を求めたいのに、
線分図をわざわざ「小」にそろえてまず「小」を求めて…
そこに10をたして「中」を求める。
もちろん間違いではありません。

ほんの少しの手間の差と感じるかも知れません。

ただ、入試本番を考えれば、
「限られた時間内にいかにスピーディーに、かつラクに解くか」
が大切なのです。

塵も積もれば山となる。
ほんの少しの工夫・意識が重なれば、
大きなアドバンテージとなり得ます。

是非、みなさんのお子様とも確認していただきたいポイントです。

 

今回はここまで。
また次回のブログでお会いしましょう！