みなさん、こんにちは。受験Dr.の亀井章三です。

今回は「難問を解く方法」です。
解くのが難しい問題は、どこに着目しどう展開していくのか。
2025年灘中入試問題（一日目）を使用して説明します。

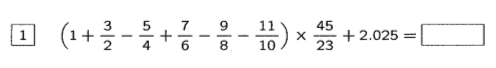
灘中（一日目）の大問１は計算問題です。
入試年度の西暦（今年であれば2025）を使用しているのが特徴的です。
難易度としては高くなく（面倒な問題＝難しい、というわけではありません）、
丁寧に計算していけば大丈夫です。

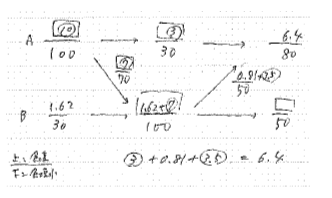
食塩水の問題ですが、標準的なやりとりの問題です。
特に捻ったところもありませんので、やり取り図を描いて解くと判断できれば大丈夫
です。分からない食塩の重さが多いため、Aの食塩の重さを⑩とおき、マルイチ算
で解く、と方向を定めましょう。

 

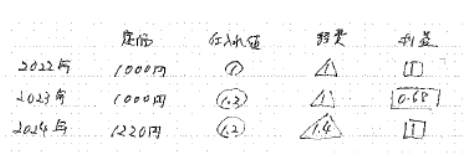
売買損益の問題ということはすぐ分かりますが、見慣れない「経費」という単語が
出ています。そのため、「経費」の扱いに注意して問題文を数式にしていくことを
考えます。割合の部分をマルイチで表します。割合が「仕入れ」「経費」「利益」
の3種類あるので、これは「3つの消去算」と判断できます。

調べ上げる問題は、「全部調べるとしたら何個になるか」と見積もることです。
4桁の整数で９の倍数でも25の倍数でもある数は、
9999÷225＝44あまり99、999÷225＝4あまり99
44－4＝40個と分かります。
40個書き出して調べることは「面倒」でしょうか？
先程も書きましたが、面倒＝難しい、ではありません。40個を書き出して確認
すれば確実に正解でき、得点できるわけです。1点を争う入試でこのように行動
できるかはとても重要です。

これは数の性質の問題です。具体的な数字を用いて考えます。
Ｂ駅行き電車が169本出たということは、電車と電車の間隔が168個あるという
ことになります。同様にＣ駅行きの間隔は70個、Ｄ駅行きの間隔は40個になり
ます。そこで、始発から終電までの時間を、168と70と40の最小公倍数840分
とし、Ｂ駅行きは5分間隔、Ｃ駅行きは12分間隔、Ｄ駅行きは21分間隔として
問題を解いていきます。

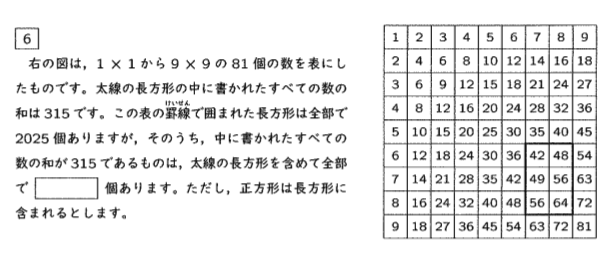
これも数の性質を利用した調べの問題です。
何か「規則」のようなものがあると推測できますが、その規則を短時間で見つける
のは難しいです。1分ほどあれこれやってみて規則が出ないようであれば先へ進む
という選択を取っても良いです。
ヒントは九九の表であることです。積を九九の形に直してみましょう。
42+48+49+56+56+64
＝6×7+6×8+7×7+7×8+8×7+8×8
＝(6+7+8)×(7+8)
このことから、１～９のうちのいくつかの和が315の約数になっていれば良いと
気づけるかどうかです。

覆面算の問題です。まずは問題文を式にすると、
EFGH　×　D　＝　１ABC２　　A～Hは０，３～９のどれか
となります。
このタイプの問題は「積の一の位」、「数の範囲」がポイントです。
H×Dの一の位が２になるので、DとHの組み合わせは
（３、４）（４、３）（４、８）（６、７）（７、６）（８、４）（８、９）（９、８）があります。
１ABC２は最大で19872、最小で10342です。これを考えられるDの値で割った
とき、商の範囲がどうなるか表にまとめましょう。

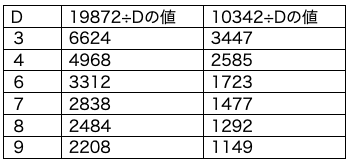
EFGHは3000以上の整数なので、この時点でDは3か4か６になり
（D、H）は（３、４）(４、３)(４、８)(６、７)　まで絞れます。
さらにD=4、H=３のとき、Eにあてはまる数がなくなるため、これも除外されます。
残り３つについてそれぞれ調べていくことになります。

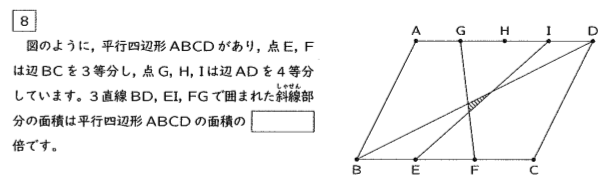
相似形と面積比の問題です。図形の問題は「方針」をしっかり決めることが大切
です。設問が「四角形ABCDに対する斜線部分（PQRとする）の面積比」なので、
・平行四辺形は長方形にして見やすくする
・具体的な辺の長さを決める
・BQ：QP：PDとER：RP：PI　を求める
と決め、後は粛々と作業を進めていきましょう。

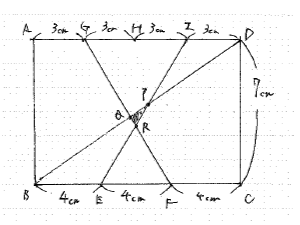
求積の問題です。辺の長さは出なさそうなので、比で解くと工夫をするかの選択に
なりそうです。円に接する正多角形の対角線の中には平行になるものがある、という
知識があれば、CDとBE、AFが平行、BCとADが平行であることが分かります。
すると、四角形BCDGが平行四辺形となり、三角形BCGと三角形CDGが合同
で同じ面積であることが分かります。このことから、他の三角形にも同じ大きさの
三角形が作れるのではないか？と考え、それを説明するための補助線を引こう、
という発想になります。

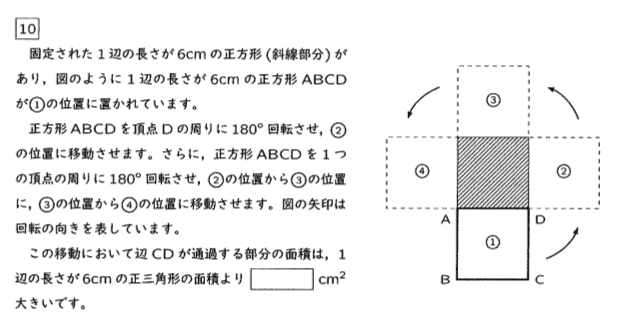
標準的な図形の回転移動の問題です。正しく作図さえできれば難しくはありません。
問題で「正三角形の面積より何㎠大きいですか」と聞かれているため、図の中に
正三角形が出てくることは予想できます。

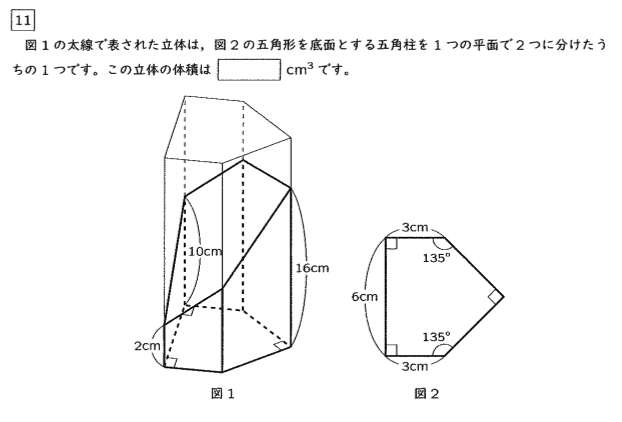
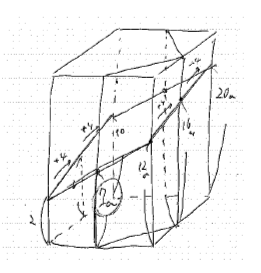
立体切断の問題です。五角柱を斜めに切断した立体なので、断頭五角柱という
立体になります。この場合、底面積×高さの平均という公式は使えないので、
３つの断頭三角柱に分けて求める、という解法になります。上位校の算数では
頻出のテーマなので、身に付けておきたいです。
135度の部分の高さを出すためには、図のように直方体を使って考えることに
なります。経験が必要な難問と言えるでしょう。

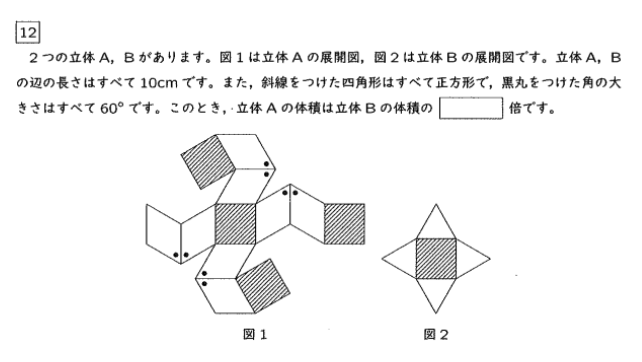
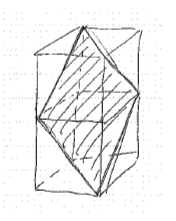
切断で作られた立体の展開図を用いた、灘中頻出問題です。
ひし形＝下の図のような直方体を切断してできる、ということを覚えているかどうか
でこの問題は決まります。
また全ての辺の長さが1㎝の四角すいの体積は、辺の長さが1㎝の正四面体の
2倍になることも「知識」として必要です。

今回は灘中2025年の問題を用いて、難問を解くためのポイントを説明しました。
くり返し出てきたことは、「知識」が必要であるということと「経験」がものを言うとい
うことです。灘中をはじめとする算数が難しい学校を目指す方は、様々な問題を
実際に解いてみることで「知識」と「経験」を身に付けていきましょう。