みなさん、こんにちは。
受験Dr.算数科の江田です。

今回は「円に引く補助線」について、
その中でも角度を求める問題を取り上げます。

さっそく例題です。
まずは基本問題から。

【例題１】
下の図のように、点Оを中心とする円があります。
図の角アは何度ですか。

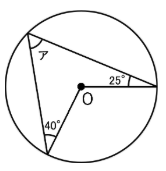
さて、ここで意識してほしいこと。
それが今回のブログのテーマ、「円に引く補助線」についてです。

「円に引く補助線といえば“半径”を真っ先に疑え！」
これが今回伝えたいこと。
これを合言葉に問題に取り組みましょう！

そう、下のように中心Оから点Pを結ぶ補助線を引くわけです。

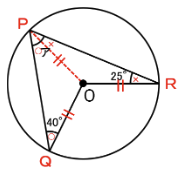
すると
OP＝OQ＝OR（すべて半径）となるので、
図のように◯どうし、✕どうしがそれぞれ同じ角度になります。
よって、角アは
40＋25＝65(度)
と求まります。

 

それでは次の例題です。
次は標準問題。

【例題２】
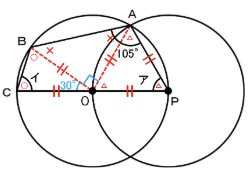
下のように、
点О、点Pを中心とする同じ大きさの円の円周が
それぞれの中心を通るように重なっています。
図の角ア、角イの大きさはそれぞれ何度ですか。

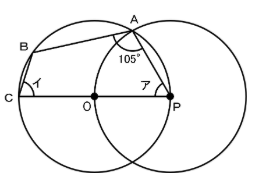
ここでも
「円に引く補助線といえば“半径”を真っ先に疑え！」
を合言葉に取り組んでみましょう。

下の図のように補助線を引きます。

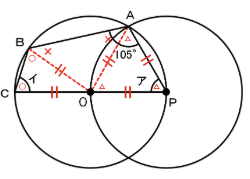
すると
OP＝OA＝OB＝OC＝PA（すべて半径）となり、
図のように◯どうし、✕どうし、△どうしがそれぞれ同じ角度とわかります。

そう、つまり三角形ＯＡＰは正三角形だったんですね！
よって、角アは
180÷3＝60(度)
と求まります。

そして、✕は
105－60＝45(度)、
角ＡＯＢは
180－45×2＝90(度)、
角ＢＯＣは
180－(60＋90)＝30(度)
と求まります。

よって、角イは
(180－30)÷2＝75(度)
となります。

ちなみに、
「四角形ＡＢＣＰの内角の和(360度)が〇✕△2つずつの合計である」
ことに気付くことができれば、
〇✕△1つずつの合計が
360÷2＝180(度)
とわかるので、角イは
180－105＝75(度)
と簡単に求めることもできます。

 

さあ、次が最後の例題です。
最後は応用問題。

【例題３】

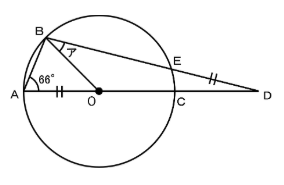
下の図において、
点Оは円の中心で、OA＝DEとなっています。
このとき、角アは何度ですか。

さあ！
ここでも
「円に引く補助線といえば“半径”を真っ先に疑え！」
が合言葉！

どこに補助線を引けばよいのか、わかりますか？
“半径”を引けそうなところ・・・

正解は・・・

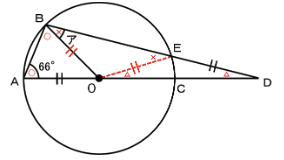
上の図のように点Оと点Eを結ぶのです。
すると
OA＝OB＝OE＝DE
となるため、
◯どうし、✕どうし、△どうしがそれぞれ同じ角度とわかりますね。

ここで
三角形ＯＤＥにおいて「外角の定理」を利用すると
✕は△2つぶん
とわかり、三角形ＯＢＤにおいて「外角の定理」を利用すると
角ＡＯＢは△3つぶん
とわかるので、下の図のように整理できます。

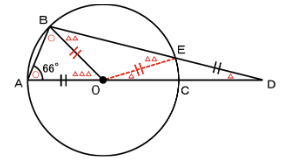
このことから、△1つは
(180－66×2)÷3＝16(度)
と求まり、角アは
16×2＝32(度)
と求められます。

いかがでしたか。
基本問題から応用問題まで、
すべて“半径”を引いて考えることがキーポイントとなっていたことが
わかっていただけたかと思います。
是非お子様に
「円に引く補助線といえば“半径”を真っ先に疑え！」
という合言葉を確認してあげてください。

きっと、問題を解く手がかりになってくれることでしょう。

今回はここまで。
また次回のブログでお会いしましょう！