こんにちは。
受験Dr.算数科講師の千葉　誠と申します。

今回は「速さとグラフ」単元の中でつまずきやすい「二者間（隔たり）グラフ」問題を解くときのコツを紹介します。

ポイントは２つあります。
1.グラフが折れている点で起きたイベント（出来事）を書き込む
2.グラフの各直線の速さを、1人の速さ・2人速さの和/差に分類して書き込む

実際に問題を解きながらこの2つのポイントを確認していきましょう

【問題】
兄と弟が家を同時に出発し、家と駅の間をそれぞれ一定の速さで1往復しました。下のグラフは、2人が出発してから弟が家にもどるまでの時間と、2人間の距離の関係を表したものです。兄は弟より速いものとして、次の問いに答えなさい。

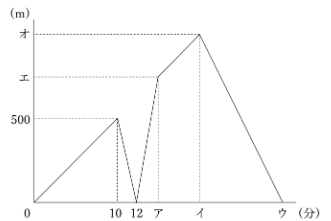
(1)兄、弟の速さはそれぞれ分速何mですか。
(2)グラフのア～オにあてはまる数をそれぞれ求めなさい。

【解説】
（ポイント1）
まず、速さの異なる2人の往復で起こるイベントを順番に考えると
2人が家を出発→速い方（兄）が駅を折り返す→2人がすれちがう→遅い方（弟）が駅を折り返す
→速い方（兄）が家に着く→遅い方（弟）が家に着く
となります。
これをグラフに書き入れます。

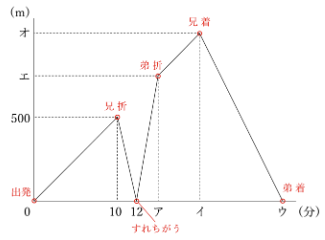
（ポイント2）
次に、各直線の速さを分類すると
0～10分→2人が同じ方向に移動しているので、距離の変化は「速さの差」＝兄－弟
10～12分→2人が反対方向に移動しているので、距離の変化は「速さの和」＝兄＋弟
12～ア分→2人が反対方向に移動しているので、距離の変化は「速さの和」＝兄＋弟
ｱ～イ分→2人が同じ方向に移動しているので、距離の変化は「速さの差」＝兄－弟
イ～ウ分→弟だけが移動しているので距離の変化は「弟1人の速さ」＝弟
これをグラフに書き込みます。

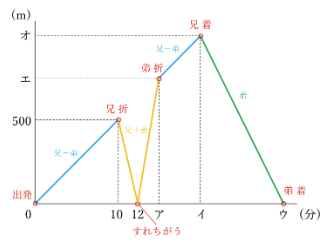
これで問題を解く準備は完了です。
(1)
距離と時間が分かり、速さが出せる0～10分と10～12分に注目すると
0～10分→500÷10＝50（m/分）・・・兄－弟（速さの差）
10～12分→500÷(12－10)＝250（m/分）・・・兄＋弟（速さの和）
2人の速さの和と差が分かったので、和差算でそれぞれの速さを求めると
(250＋50)÷2＝150（m/分）・・・兄
250－150＝100（m/分）・・・弟
A.  兄・・・分速150m、弟・・・分速100m

(2)
時間を調べる時には書き込んだイベントが役に立ちます。
兄が折り返したのが10分後→兄は片道10分
→往復は10×2＝20（分）→兄が家に着くのは20分後
→イ＝20

片道の距離は150×10＝1500（m）
弟の片道の時間は1500÷100＝15（分）→弟が折り返したのは15分後
→ア＝15

弟は片道15分→往復で15×2＝30（分）
→弟が家に着くのは30分後
→ウ＝30

時間がすべてわかったので距離について調べると
兄は10分後に折り返してから弟が折り返すア（15分後）まで、
兄は15－10＝5（分）移動しているので、ア（15分後）の2人の間の距離は
150×5＝750（m）
→エ＝750

イ～ウ（20～30分）で弟は30－20＝10（分）移動しているので
100×10＝1000（ｍ）
→オ＝1000

「二者間グラフ」では2人の移動の様子を1本のグラフで表すため、何が起こっているのかを把握するのが困難です。
今回紹介した2つのポイント「イベント・速さの分類」を書き込むことによって、グラフの各時間での情報が整理され、各段に解きやすくなるので、ぜひ参考にしてみてください。

それでは、失礼します。