こんにちは。
受験Dr.の科学大好き講師、澤田重治です。

皆さんは、理科の問題演習をしていて、自分の答えが「12」なのに、
模範解答には「12.0」と書いてあって困った……というような経験はありませんか？

算数では、省略しなければならないと教わったはずなのに、
なぜか理科ではよく出てくる「.0」――今回はその謎に迫りたいと思います。

 

理科実験での約束

理科というのは、「理（ことわり＝自然界のルール）を学ぶ学問」という意味です。
つまり、先に自然現象があって、それを人間が調べることから始まる学問なのです。

その意味で、理科には「観察」や「実験」が欠かせません。

そして、実験において正確なデータを取るためには、
全世界の科学者さんたちが計器の数値を読むときの
共通のルールが必要になってきます。

そのルールとは、
「最小目盛りの10分の１まで目分量で読む」　というもの。

つまり、皆さんの筆箱に入っている一般的な定規で長さをはかる場合なら、
一番小さな目もりは「１mm」ですから、
その10分の１である「0.1mm」の位まで目分量（見た感じ）で読み取るのです。

 

　理科実験での 「12」 と 「12.0」 と 「12.00」 のちがい

実際の例を見ながら考えてみましょう。

下の図のように、最小目盛りが10cmの大ざっぱな定規があったとします。

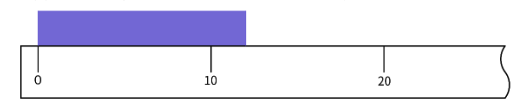
この定規で長さを測ると、10～20cmの間を目分量で10等分し、
そのうちの２目盛りくらい……と判断して、「12cm」と読むことになります。
いかにも不正確ですよね。

 

次に、下の図のように、最小目盛りが１cmの定規で測ってみます。

最小目盛りが１cmなので、その10分の１である0.1cm（＝１mm）まで読むのですが、
12の目盛りちょうどに見えますね。
この場合は、「12.0cm」と読み取ることになります。
かなり正確性が増したと思いませんか？

最後に、皆さんが持っている最小目盛り１mmの定規の場合です。

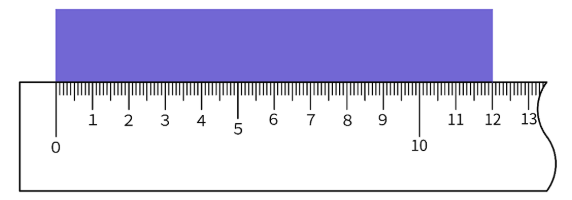
最小目盛りの10分の１ということは0.1mm（＝0.01cm）まで読むことになりますが、
これもぴったり12の目盛りに重なって見えますから、「12.00cm」と読み取ります。

いずれの場合も、書いてある最後の位は目分量だから正確ではないということなのです。
この誤差の必要性こそが、「理論値の算数」と「実験値の理科」の大きなちがいなのでしょう。

 

結局、何のための 「.0」 だったのか？

このように、同じ物体の長さを測っていても、使用した定規によって、
その正確さは大きくちがってくるということが分かると思います。
そしてそれは、得られたデータの信頼性にも関わってきます。

だから、理科の世界では、そのデータの正確さをはっきりとさせるために、
算数では省略する 「.0」 や 「.00」 をわざわざ書いていたのです。

また、これらのデータを利用して計算した場合も同様です。
およその数値を使って計算しているのですから、
その計算結果については、どうしても誤差が含まれてしまいます。

そこで、どのケタの数値までが信用できるかという考え方が必要になります。
これを「有効数字」と呼んでいます。

 

では、入試の解答の場合には、どのように扱われるのでしょうか？

実際には、ほとんどの学校で入試の採点基準を公表していないので、
確定的なことは言えません。

しかし、小学校の学習指導要領で「有効数字」に触れていないので、
受験生も知らないはずですから、おそらく「.0」の有無は、多くの学校で
採点には関わっていないと思います。

ただし、問題文の中で、「小数第１位まで答えなさい」などというように
指定があれば、もちろんそれに従う必要がありますので注意してください。

心配な人は、問題中で与えられたデータが小数第１位までだったら、
自分が答えを書く時にも「12.0」などと
小数第１位まで書くようにしておけば問題はないでしょう。

 

次回もまた、楽しくて中学受験の役に立つ、身近な科学の話をお届けします。
どうぞお楽しみに！