みなさん、こんにちは。
受験Dr.算数科の江田です。

前回に引き続き、今回も中学受験算数において必ず頭に入れておきたい図形についてのお話。

前回は「30゜，60゜，90゜の直角三角形」という平面図形でしたが、
今回は立体図形のお話。

それは「1：1：2の三角すい」です。
特に6年生は現時点ですぐにピンときてほしい、
主に立体切断の問題で多く見かけるこの立体。

下の図のような立体です。

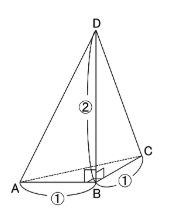
この三角すいを、三角形ＡＢＣを底面として見ると
底面が直角二等辺三角形で高さが辺ＡＢや辺ＢＣの2倍の長さ
になっていますね。
このような立体を「1：1：2の三角すい」と呼ばせてもらいます。

この三角すい、展開図にすると…

のように、きれいな正方形になります。

このことを利用した問題が中学受験算数には多く見られるんです。
先ほど「主に立体切断の問題で多く見かける」とお伝えしましたが、
今回のブログでは切断は考えず、シンプルな問題だけ扱いますね。

たとえばこんな問題。

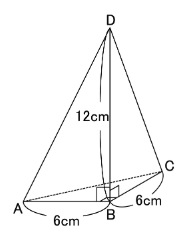
上の図のような三角すいがあります。
この図の三角形ＡＣＤの面積は何㎠ですか。

これは先ほどのように展開図を考えれば…

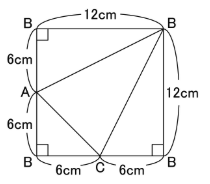
このような図形となるので、
正方形全体の面積から三角形ＡＢＣのまわりにある3つの三角形の面積を引くことで
三角形ＡＢＣの面積が求まります。

よって、三角形ＡＢＣの面積は
12×12－(6×6÷2＋6×12÷2×2)＝54(㎠)
とわかります。

なお、この三角形ＡＢＣの面積は

ことも覚えておくとよいでしょう。

覚えておけば
12×12×＝54(㎠)
と、簡単に求めることができるので便利ですね！

いかがでしたか。

前回の
「30゜，60゜，90゜の直角三角形」
は平面図形の問題にとりかかる際に、
今回の
「1：1：2の三角すい」
は立体図形の問題(特に切断の問題)にとりかかる際に、
必ず頭の片隅に置いておきたいものです。

今回はここまで。
それではまた次回お会いしましょう！