みなさん、こんにちは。受験Dr.の桑田陽一です。

今回は、前回の続き。
2025年2月に行われた東京大学の入試を題材に紹介した問題の解決編です。
まずは、問題を再確認しましょう。

 

問題

白玉2個が横に並んでいます。コインを用いて次の手順をくり返し、白玉または黒玉を横一列に並べていきます。

手順

コインを投げ、表が出たら白玉、裏が出たら黒玉を、それまでに並べられている一番右にある玉の右隣におく。そして、新しくおいた玉の色がその1つ左の玉の色と異なり、かつ2つ左の玉の色と一致するときには、新しくおいた玉の1つ左の玉を新しくおいた玉と同じ色の玉に取りかえる。

例えば、手順を2回行い、コインが裏、表の順に出た場合には、白玉が4つ並びます。

(1)手順を3回行ったとき、右から2番目の玉が白玉であるようなコインの表裏の出方は何通りですか。
(2)手順を5回行ったとき、右から2番目の玉が白玉であるようなコインの表裏の出方は何通りですか。
(3)手順を8回行ったとき、右から1番目と2番目の玉がともに白玉であるようなコインの表裏の出方は何通りですか。

（2025　東京大学　文科第3問　改）

 

前回は、この(2)までを考えました。

その中で、「右端の2個だけ」に注目した樹形図を考えてみること、

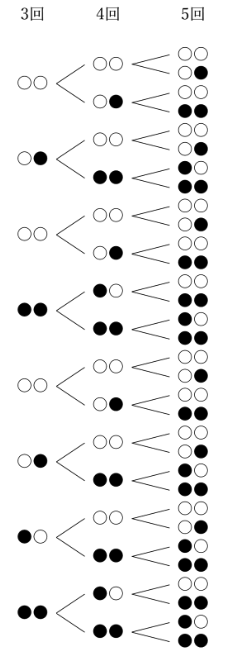
そして、この樹形図の5回目のところには、「○○」が11個、「○●」が6個、「●○」が5個、「●●」が10個あること、
さらに、この樹形図には以下の4パターンの枝分かれのみが繰り返し現れていること、

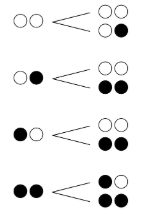
(3)を解決するためのヒントとして、この辺りを前回の最後に確認しました。
これらのことを使って、今回は(3)を解決していきましょう。

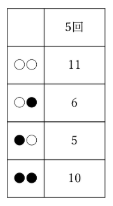
操作を5回行った後の樹形図に現れている枝の数を、いったん表にまとめます。
さてここで、例えば○○の枝は11本。そしてこれらは全て、

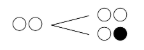
このように枝分かれするのでした。
つまり、5回目に現れている11本の○○から、6回目の枝として○○と○●が11本ずつ「産み出される」ことになります。

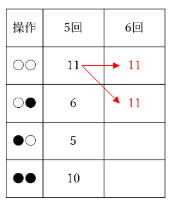
同じように、

○●からは、○○と●●が産み出されます。

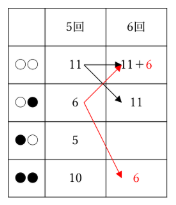
さらには、

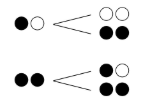
●○から○○と●●、●●から●○と●●が産まれるので、

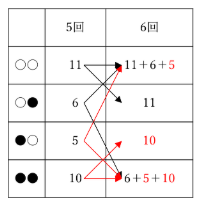
このように表にまとめられます。足し算を計算してしまえば、

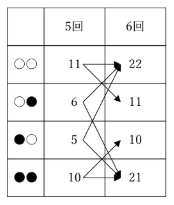
実際に樹形図を書かなくても、このように6回目に現れる枝の数を求めることができました！

同じように考えると、7回目に現れる枝の数は、

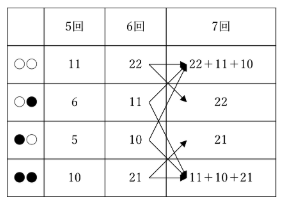
つまり、

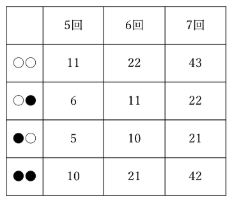
さらに8回目も、

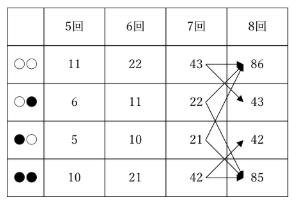
このように、計算で場合の数を求めることができました。
(3)で求めるのは、「手順を8回行ったとき、右から1番目と2番目の玉がともに白玉であるようなコインの表裏の出方」でしたから、この表の一番上にある86通りが答えだと分かりました！

勉強が進んでいる受験生の中には、「似たような考え方を使う問題をやったことがある！」と感じた人もいるかもしれません。
実際に、中学受験算数の場合の数でも、同じ色が隣り合わないようにボールを並べたり、正四面体の頂点を点が移動したり、というような設定で、前の回を利用して次の回の場合の数を求める問題が出題されています。

数学用語では「漸化式(ぜんかしき)」という考え方。元々の東京大学の出題は、「漸化式」を本格的に使う問題でしたが、その雰囲気を味わうことができる内容で紹介した1題でした。
楽しんでもらえたでしょうか？

今回は、ここまで。次回もお楽しみに。