皆さんこんにちは。
受験ドクター講師の勝山利信です。

さて、今回は前回に引き続き問題対応力の鍛え方についてお話しします。
前回は関係式を図示化することで、考え方が見えてくる例として食塩水の濃さに関してお話ししました。

＜食塩水の濃さに関する面積図＞

混ぜる前後の図を重ねることで、計算するべきことが見えてきます。

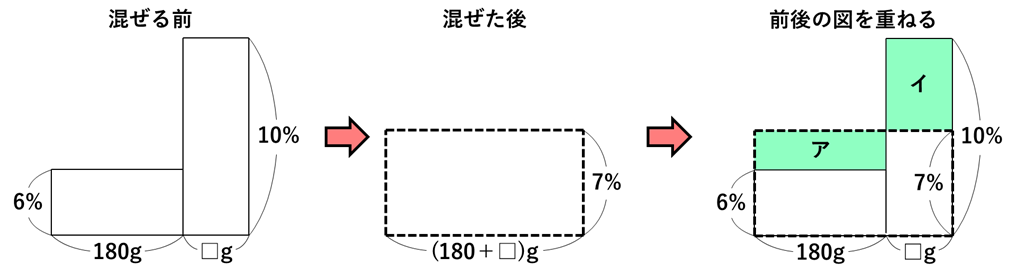
重要なポイント
・算数では「等しさ」を利用して物事を考えていくことが基本姿勢
⇒混ぜる前後で食塩の合計量（図における面積）が変わらない

このことを生かして、少し工夫して出題された問題を見てみましょう。
比の基礎知識は学んでいるものとしてお話しを進めていきますが、まだ学んでいない場合でもどのようなところに着目しているのか参考にしてみてください。

非常にシンプルな問題ですが、混ぜる食塩水の濃さが両方ともわかっていないので、混ぜる量を比に従って適当に設定したとしても、なかなかゴールが見えてこないタイプの問題です。

「どうすればよいか？」

新しいパターンの問題にぶつかったときほど、基本に立ち返って考えてみましょう。
まずは、素直に条件を図示化してみます。

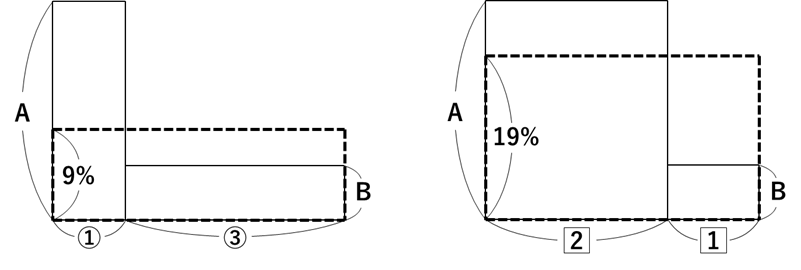
食塩水Aが多いとき濃い食塩水ができるので、食塩水Aの方が食塩水Bより濃いことは分かっています。
最初は前回と同じく、食塩の量が混ぜる前後で等しいので、2ヶ所の長方形の面積が等しくなっていることに着目しましょう！すると今回は、面積が等しいのであれば、横の長さの比と縦の長さの比が逆転することから、縦の比率を考えることができます。

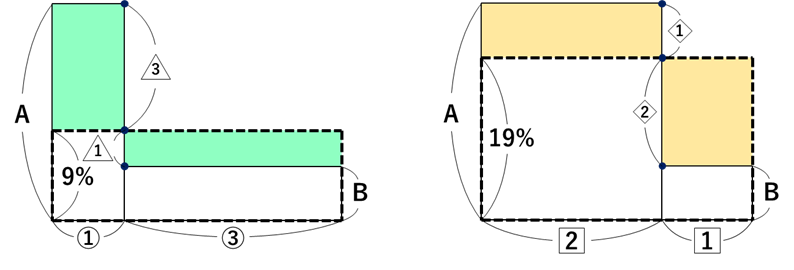
ここまでくれば最後の仕上げです。
食塩水Aと食塩水Bの濃さの差が、３：１と１：２に分けられているので、比の和をそろえて全体を１２ととらえます。すると、９％と１９％の差の１０％が５に当たることが分かるので、１に当たる大きさは２％、食塩水Aの濃さは９＋２×９＝２７％、食塩水Bの濃さは９－２×３＝３％であることがそれぞれ求められます。

大きさが等しい部分が異なる比率で分けられているときに、和をそろえて計算を進める場面は多いので、他の問題でも確実に対処できるようにしておきましょう。問題ごとの解き方を１：１で覚えるのではなく、様々な「見える化」のテクニックを使えるようにトレーニングを重ね、問題に対応する力を養っていきましょう！

目指せ問題対応力UP！
それでは、またお会いしましょう！