こんにちは。
受験Dr.算数科講師の千葉　誠と申します。

今回は「円とおうぎ形」の問題における補助線の引き方についてお話します。
補助線が必要な問題は、問題の図に自分で線を描き加えないと解くことができませんが、算数が苦手なお子さんは、どこに線を描けばいいのかわからず、つまずいてしまうことが多いです。
しかし、中学受験の「円とおうぎ形」の問題においては、補助線を引くための明確な方針が存在します。
それは、「円（おうぎ形）の中心から円周（弧）上の頂点に引く」というものです。
円は「円周上のどの点も中心からの距離が等しい」という性質を持ち、「円とおうぎ形」の問題のほとんどはこの性質を利用します。
そのため、「円とおうぎ形」の問題では、この性質を利用できる図形を見つけるために、中心と円周を結ぶ線、つまり半径を補助線として引くことがセオリー（定石）となっています。
実際の入試問題で確認してみましょう。

【問題】　渋谷教育学園渋谷中学校2025年度入試問題より抜粋
下の図のような半径が10cmの円があります。円周上の点は円周を12等分しています。影のついた部分の面積は何㎠ですか。

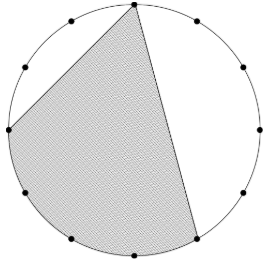
【解説】
図に中心を表す点が描かれていないので、中心も自分で描き入れたうえで、「円の中心から円周上の頂点に引く」という方針にしたがって補助線を引きます。

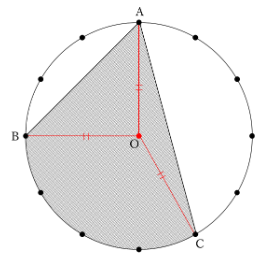
こうすることで、影の部分が三角形ABO、三角形ACO、おうぎ形BOCの3つ図形に分割できました。
また、OAとOBとOCが円はそれぞれ円の半径なので、
OA＝OB＝OC＝10cm
より、三角形ABOと三角形ACOはどちらも二等辺三角形です。
また、円周上の点が円周を12等分する点であることに注意して角度を調べると、
角AOB＝360×＝90(度)
角AOC＝360×＝150(度)
角BOC＝360×＝120(度)
角OAC＝角OCA＝（180－150）÷2＝15(度)

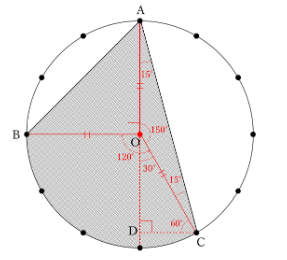
三角形ABOは直角二等辺三角形なので、面積は、
10×10×＝50(㎠)
三角形ACOは15度・15度・150度の二等辺三角形で、頂点Ｏの外角は30度です。
頂点Ｃから辺ＡＯの延長線に垂直に線を引き、交点をＤとすると、
ＣＤの長さは、辺ＡＯを底辺としたときの高さになります。
三角形ＯＣＤは30度・60度・90度の直角三角形なので、これが正三角形の半分であることを利用すると、
CD＝10×＝5(cm)
よって三角形ＡＣＯの面積は、
10×5×12＝25(㎠)
おうぎ形BOCは半径10cm、中心角120度のおうぎ形なので、面積は
10×10×3.14×＝104 (㎠)
以上より、影の部分の面積は、
50＋25＋104＝179(㎠)

平面図形においては二等辺三角形や正三角形のように、同じ長さの辺を持つ図形の性質を利用して解く問題が多くあります。
これらの特殊な性質を持つ図形を見つけることが補助線の役割であり、「円とおうぎ形」の問題においては「円（おうぎ形）の中心から円周（弧）上の頂点に引く」というのが最も有効な補助線の引き方になります。
この方針を知っていることで、対応できる問題の幅が大きく広がりますので、ぜひ身に着けておきましょう。

それでは、失礼します。