みなさんこんにちは。受験ドクターの石田新一です。

「カロリー」というと食事での摂取カロリーが思い浮かぶと思いますが、１日の必要摂取カロリーは、年令、身長、体重、日々の運動量によって異なります。ちなみに、３０歳成人男性、身長１７０㎝、体重６３kg、電車通勤だとすると、１日に必要な摂取カロリーは、約２４００キロカロリーです。
理科のテストで出題されるカロリー計算の問題は、「水１gの温度を１℃上げるのに必要なカロリーは、１カロリー(cal)である」という前提で出題されます。
今回は、カロリー計算についての基本的な考え方をお伝えしたいと思います。

＜考え方＞
水１gの温度を１℃上げるのに必要な熱量が１calです。２００gの水の温度を１０℃から
８０℃へ７０℃分上げるので、必要な熱量は７０℃×２００g＝１４０００calとなります。

＜考え方＞
温度１℃の水１gが持っている熱量を、１℃×１g＝１calと考えます。２０℃、１００gの水は
２０℃×１００g＝２０００calの熱量をもっていて、８０℃、２００gの水は８０℃×２００g＝１６０００calの熱量を持っています。この２つの熱量を合わせると１８０００calになります。この熱量を、最終的には水３００gがもっているということになるので、１８０００cal÷３００g＝６０℃となります。
以上のことをグラフで表すと、次のようになります。

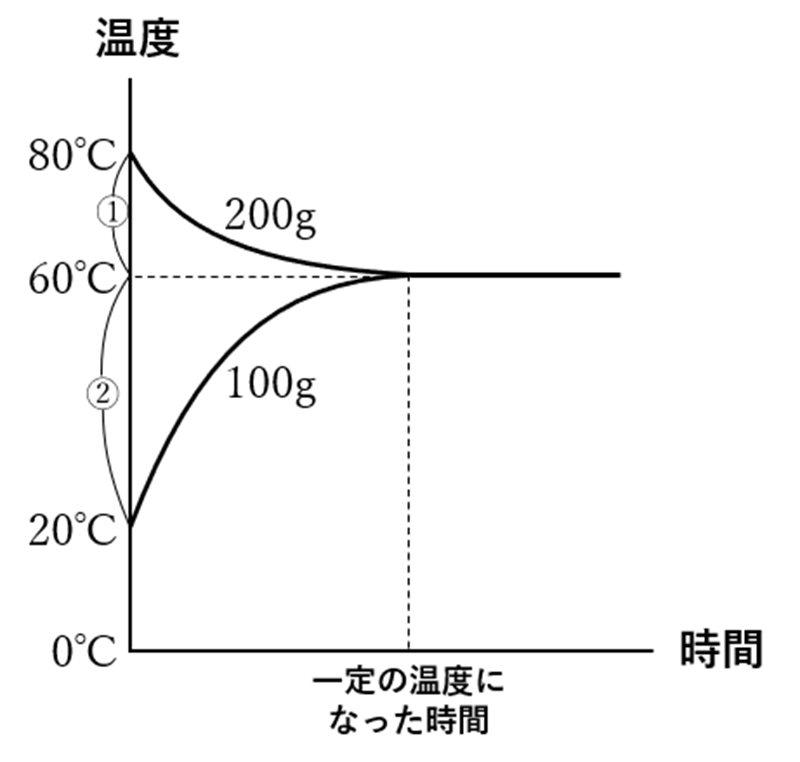
グラフを見ると、水の重さと温度変化の比が「逆比」になっていることが分かります。そこで、算数の「食塩水」の問題でよく利用する「てんびん図（加重平均）」で、この問題を解いてみると以下のようになります。
　

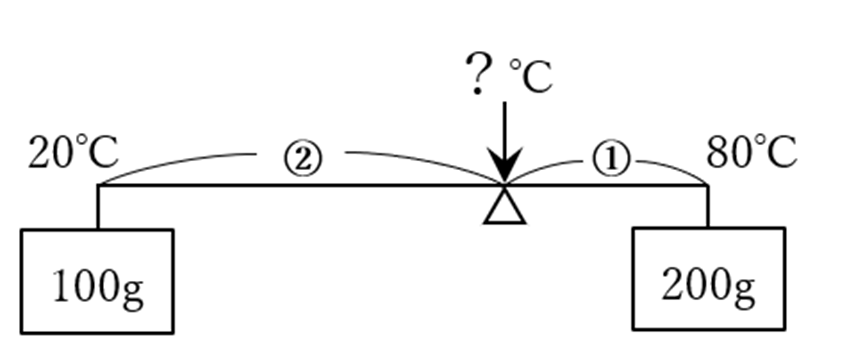
求めたい？℃を支点とすると重さの比が１：２なので、支点からの距離の比は「逆比」になるので、図のように②：とになります。③にあたる温度が８０℃－２０℃＝６０℃なので、
③＝６０℃、①＝２０℃となります。２０℃に②の４０℃を加えた位置、または８０℃から①の２０℃を引いた位置が支点となるので、求めたい？℃は６０℃となります。　
　　

＜考え方＞
例題２と同様に、温度１℃の水１gが持っている熱量を、１℃×１g＝１calと考えます。

Aのビーカーの水が持っている熱量は、２５℃×２４０g＝６０００cal
Bのビーカーの水が持っている熱量は、６５℃×８０g＝５２００cal
Cのビーカーの水が持っている熱量は、９０℃×１２０g＝１０８００cal　となります。

この３つの熱量を合わせると２２０００calになります。この熱量を、３つのビーカーに入っていた水の合計４４０gがもっているということになるので、２２０００cal÷４４０g＝５０℃となります。

　また、てんびん図で解くとすると、まずAとBの水を混ぜたときの温度は３５℃になります。次に、３５℃、３２０gの水とCを混ぜると考えます。すると、答えは５０℃となります。
ただし、てんびん図を２回使うことになるので、（カロリーの合計）÷（水の重さの合計）で計算する方が速いと思います。
さらに、「面積図」で解くこともできますが、面積図自体を書くのに時間がとられてしまいますので面積図は使わない方が良いでしょう。
　　　　　　　　
以上のように、２つのものを混ぜるときは「てんびん図」が有効で、３つ以上のときは、カロリーの合計を出し、水の重さの合計で割る方法が良いと思います。

模試、入試では、限られた時間の中で解答しなければなりませんので、問題に合わせて、
「解き方」を変える必要があります。他の理科の計算問題、算数の問題に対して、できるだけ多くの解法を身に着け、「解法の使い分け」ができるようにすることを意識しながら、今後の学習を進めて頂ければと思います。