みなさん、こんにちは。
受験Dr.算数科の江田です。

前回・前々回と連続して
「頭に入れておくべき図形」についてお話しました。

今回は、前回お話した「1：1：2の三角すい」の実戦編です。

まずは前回の内容をさらっとおさらい。

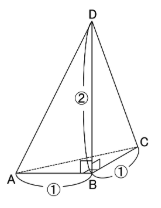
これが「1：1：2の三角すい」でしたね。
そして、この三角すいを展開図にすると

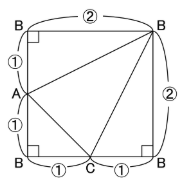
のように、きれいな正方形になりましたね。
また、この
というお話までしました。

今回はこのことを大いに利用する立体切断の問題を扱いましょう。

【問】下の図のような1辺12㎝の立方体があります。

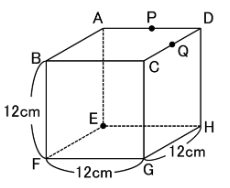
辺ＡＤの真ん中の点をＰ、辺ＣＤの真ん中の点をＱとして、この立方体を3点Ｅ、Ｐ、Ｑを通る平面で切断します。これについて、次の問いに答えなさい。
(1) 切断面の面積は何㎠ですか。
(2) 2つに分けられた立体のうち、点Ｈを含む方の立体の体積は何㎤ですか。
(3) 点Ｈから(1)で求めた切断面に垂直におろした線の長さは何㎝ですか。

 

という問題。

 

さっそく解説していきますが、
今回は「1：1：2の三角すい」のポイントのお話のため、
切断面の考え方は割愛させていただきますね。

 

まずは(1)の切断面の面積から。
切断面は下の図のような等脚台形(台形と答えても可)になりますね。

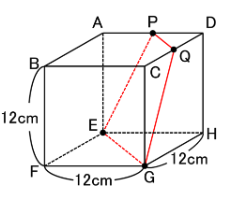
さて、この切断面の面積はどのように求めていけばよいのでしょう。
今回の切断面は「台形」ですから、その切断面の辺を下の図のように延長すれば
三角すいを作ることができますね。

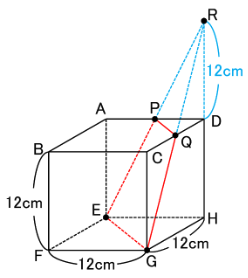
ちなみに
「切断面が台形、五角形、六角形の場合は、切断面を延長すると三角すいができる」
ということも覚えておくといいですよ！

さて、これで何か見えてきましたかね…

 

そう！
下の図の三角すいＲ-ＥＧＨと三角すいＲ-ＰＱＤがどちらも
「1：1：2の三角すい」になっていますね！

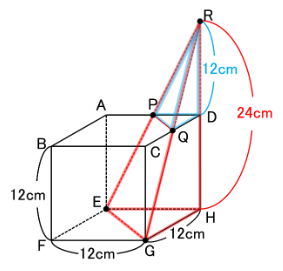
このことに気付けば…
三角形ＲＥＧの面積は
三角すいＲ-ＥＧＨの展開図となる1辺24㎝の正方形の面積のですから
24×24×＝216(㎠)
と求まりますね。

同じように、三角形ＲＰＱは
三角すいＲ-ＰＱＤの展開図となる1辺12㎝の正方形の面積のですから
12×12×＝54(㎠)
と求まります。

よって、切断面である台形ＰＥＧＱの面積は
216－54＝162(㎠)
とわかります。
(※相似比から面積比を用いて216×＝162と求めることもできます。)

次に(2)の問題。
点Ｈを含む方の立体の体積は
「三角すいＲ-ＥＧＨの体積から三角すいＲ-ＰＱＤの体積を引く」
ことによって求められます。
よって、
12×12÷2×24×＝576(㎤)　…　三角すいＲ-ＥＧＨ
6×6÷2×12×＝72(㎤)　…　三角すいＲ-ＰＱＤ
576－72＝504(㎤)
とわかります。
(※相似比から体積比を用いて12×12÷2×24××＝504と求めることもできます。)

 

そして最後の(3)の問題。
点Ｈから切断面に垂直におろした線とは…

イメージできますか？
下の図のＨＩのような線です。

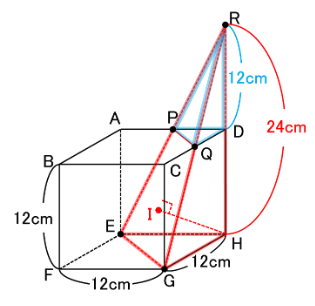
さて、気付くでしょうか。

この垂線ＨＩは、三角すいＲ-ＥＧＨの
「底面を三角形ＲＥＧとして見たときの高さ」
になっているんですね！

三角形ＲＥＧは(1)の途中で216㎠と求めていましたし、
三角すいＲ-ＥＧＨの体積も(2)の途中で576㎤と求めていたので、
216×ＨＩ×＝576
という式が立ち、これを逆算することでＨＩの長さは
576÷÷216＝8(㎝)
と求められます。

 

いかがでしたでしょうか。
「1：1：2の三角すい」ががっつり関わっていたことがおわかりいただけたと思います。

前々回の「30°,60°,90°の直角三角形」もそうですが、
常に頭の片隅に置いておかないと、なかなかすぐに気付けないものです。

是非、今後も意識して受験勉強に取り組んでもらいたいところです。

今回はここまで。
それではまた次回お会いしましょう！