こんにちは。
受験Dr.算数科講師の千葉　誠と申します。

今回は「三平方の定理」についてお話します。
三平方の定理（別名：ピタゴラスの定理）は、
ある直角三角形の最も長い辺（斜辺）の長さをa、他の2辺の長さをそれぞれb、cとすると、
a×a＝b×b＋c×c
が成り立つという定理です。

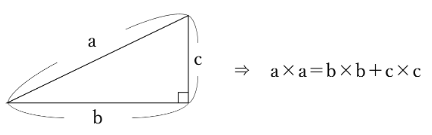
中学数学で学習する内容なのですが、小学校で習う算数の知識だけで証明できる証明法を紹介します。
この証明法は平面図形の求積の工夫の問題でよく使われるテクニックである
「斜辺を一辺とする正方形の作図」と「移しかえ」を利用したものです。

三平方の定理の証明

ある直角三角形の最も長い辺（斜辺）の長さをa、他の2辺のうち長い方の辺の長さをb、短い方の辺の長さをcとします。

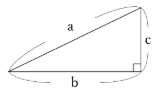
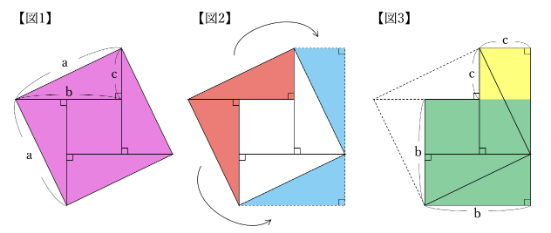
まず、【図1】のように、この直角三角形と合同な4つの直角三角形をならべて、1辺の長さがaの正方形を作ります。
この正方形の面積はa×aです。
次に、【図2】のように赤い部分の直角三角形2枚を青い部分に移しかえます。
すると、【図3】のように1辺の長さがbの正方形と、一辺の長さがcの正方形を組み合わせた図形ができます。
この図形の面積はb×b＋c×cです。
移しかえる前後で面積は変化しないので、
a×a＝b×b＋c×cとなります。

同様のテクニックを利用する問題を用意しましたので解いてみて下さい。

問題

早稲田大学高等学院中学部2025年度入試問題より抜粋
半径の長さが30cmの円と3つの合同な正方形が次の図のような位置にあります。

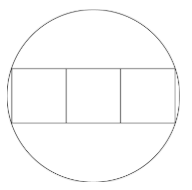
このとき、正方形1つ分の面積を求めなさい。

解説

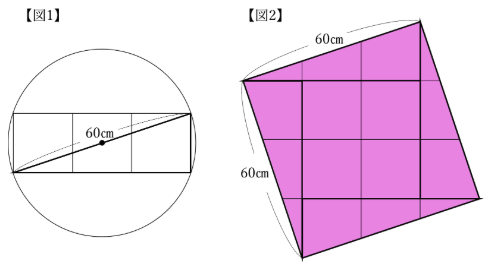
円の半径は30cmなので、直径は60cm。
まず、【図1】のように、3つの正方形でできる長方形に対角線を引くと、斜辺が60cmの直角三角形ができます。
【図2】のように、この直角三角形を4つならべて1辺60cmの正方形をつくります。
この正方形の面積は、60×60＝3600(㎠)です。

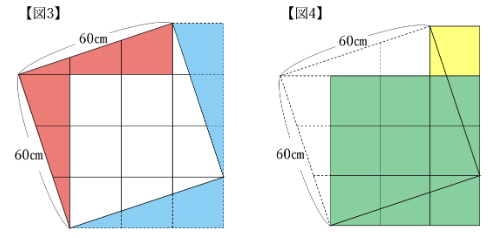
次に、【図3】のように赤い部分の直角三角形2枚を青い部分に移しかえます。
すると、【図4】のような図形ができます。
緑色の部分は3×3で正方形9個分の面積、黄色の部分は1×1で正方形1個分の面積なので、この図形の面積は正方形10個分になります。
移しかえる前後で面積は変化しないので、3600㎠が正方形10個分の面積です。
よって、正方形1つ分の面積は、
3600÷10＝360(㎠)

三平方の定理を知らないと解けない問題は中学入試ではほぼ出題されませんが、証明で利用した「斜辺を一辺とする正方形の作図」と「移しかえ」のテクニックは平面図形の応用問題で求められることが多いので、ぜひ身に付けておきましょう。

それでは、失礼します。