みなさん、こんにちは。
受験Dr.算数科の江田です。

今回は立体図形「回転体」についてのお話。

以前、
“小さな正方形”の集まりを回転させてできる立体の体積
についてお話したことがありました。

簡単におさらいをしておくと…

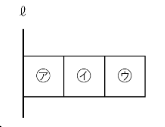
上の図のような
3つの同じ大きさの正方形㋐～㋒が直線ℓを軸に1回転したときにできる立体
の体積を考えるとき、

㋐の正方形が1回転してできる立体
㋑の正方形が1回転してできる立体
㋒の正方形が1回転してできる立体
の体積の比が「1：3：5」になる

というものでした。

同じように考えると、
㋐、㋑、㋒よりもさらに外側に正方形がついた場合、
それぞれの正方形が1回転してできる立体の体積の比は

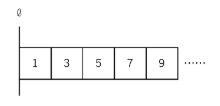
となっていきます。

 

今回はその応用編。

次のような問題を考えてみます。

【問】
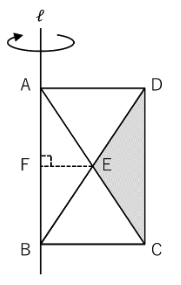
下の図のように、長方形ＡＢＣＤに2本の対角線を引きました。
この長方形ＡＢＣＤを、直線ℓを軸に1回転させたとき、
三角形ＣＤＥが通過してできる立体の体積は、
長方形ＡＢＣＤが通過してできる立体の体積の何倍ですか。

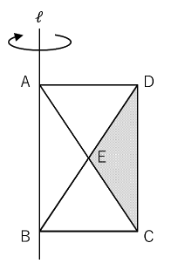
いかがでしょう。
まずは回転したときの図をイメージしましょう。

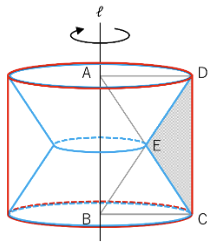
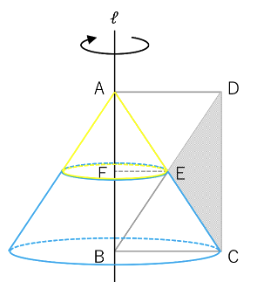
上の図のように、
長方形ＡＢＣＤが通過してできる立体は赤色の円柱、
三角形ＣＤＥが通過してできる立体は
「赤色の円柱から円すい台2つ(青色の部分)を引いたもの」
となります。

ここで、下の図のように
点ＥからＡＢに垂線を引き、ＡＢとの交点を点Ｆとします。

すると
三角形ＡＥＦが通過してできる立体は下の図の黄色の円すい、
三角形ＡＢＣが通過してできる立体は下の図の黄色と青色を合わせた円すい
となりますね。

この
「黄色の円すい」と「黄色と青色を合わせた円すい」は相似な立体であり、
相似比が1：2であるため、
体積比は(1×1×1)：(2×2×2)＝1：8
とわかります。

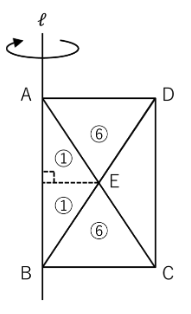
三角形ＡＥＦが通過してできる立体と三角形ＢＥＦが通過してできる立体は
向きが逆さになっているだけの同じ円すいなので…
三角形ＡＥＦが通過してできる立体と
三角形ＢＥＦが通過してできる立体と
三角形ＢＣＥが通過してできる立体の体積の比は
1：1：(8－1×2)＝1：1：6
と求められます。
また、三角形ＡＤＥが通過してできる立体は
三角形ＢＣＥが通過してできる立体と全く同じものなので…
それぞれの部分が通過してできる立体の体積比は
下のようにまとめることができますね。

次に
三角形ＡＢＣが通過してできる立体と
長方形ＡＢＣＤが通過してできる立体を考えます。

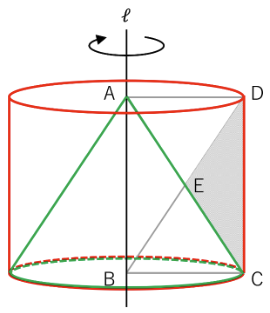
三角形ＡＢＣが通過してできる立体は上の図の緑色の円すい、
長方形ＡＢＣＤが通過してできる立体は上の図の赤色の円柱
ですね。

この2つの立体は
底面積は同じ、高さも同じですが
「柱体」と「すい体」なので、
体積比は3：1
となります。

よって、長方形ＡＢＣＤが通過してできる立体(赤色の円柱)の体積は、
先ほどまとめていた体積比(1：1：6：6)の数値を使って表すと
(1＋1＋6)×3＝24
と求められ、
三角形ＣＤＥが通過してできる立体の体積は
24－(1＋1＋6＋6)＝10
とわかります。

以上のことから、
あらためてそれぞれの部分が通過してできる立体の体積比をまとめると
下の図のようになります。

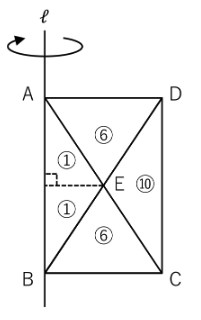
よって、

三角形ＣＤＥが通過してできる立体の体積は、
長方形ＡＢＣＤが通過してできる立体の体積の
10÷24＝(倍)
と求められます。

いかがでしたか。

今回はこのように「体積比」をとらえてほしいことから、
実際の長さなどを一切与えずに、体積の割合を問う問題にしました。
そのため、難易度は高い1問でしたが、
「比を使いこなす」ことができると計算処理が非常にラクになる
場面というのはとても多いため、
比(割合)を意識するクセをつけさせる1つのきっかけとして
今回の問題が役立てばとも思っています。

今回はここまで。

また次回のブログでお会いしましょう。