みなさん、こんにちは。受験Dr.の桑田陽一です。
7月の講師ブログをお届けします。

季節はすっかり夏。夏期講習に突入したところですが、「中学受験生も解ける大学入試数学」シリーズをもう少し続けます。

今回は、2025年2月25日に行われた京都大学の入学試験から、1題を紹介します。

問題

nは正の整数とする。1枚の硬貨を投げ、表が出たら1、裏が出たら2と記録する。この試行をn回繰り返し、記録された順に数字を左から並べてn桁の数Xを作る。ただし、数の表し方は十進法とする。このとき、Xが6で割り切れる確率を求めよ。(2025京都大学　文系　大問3)

問題の意味は取れそうですが、中学以降で学習する「確率」の問題であるため、残念ながら中学受験生がこのまま解くことはできません。

前回までと同じように、中学受験生向けに「場合の数」の問題に改めてみます。

 

問題(改)

1枚の硬貨を投げ、表が出たら「1」、裏が出たら「2」と記録することを何回か繰り返します。記録された順に数字を左から並べてできる何桁かの整数をXとします。
例えば、3回硬貨を投げて、表→裏→表の順で出たとき、X＝121です。

(1)硬貨を3回投げたとき、3桁の整数Xが3で割り切れるような表裏の出方は何通りですか。
(2)硬貨を5回投げたとき、5桁の整数Xが3で割り切れるような表裏の出方は何通りですか。
(3)硬貨を8回投げたとき、8桁の整数Xが6で割り切れるような表裏の出方は何通りですか。

ん？こうしてみると、何だか前回見た東京大学の問題に似てる？

そうですね。
中学受験の算数の問題としては様々な解法が考えられるのですが、この問題でも前回と同じような考え方を用いることが出来ます。

解いてみたくなった人は、ぜひ紙と鉛筆を用意してチャレンジ！

…
…
…
…
…

では、解説です。

解説

(1)
「3で割り切れる」、つまり「3の倍数」の見分け方といえば、「それぞれの位の数字の和が3の倍数」になることですね。
か「2」を3つ並べて、それらの和が3の倍数になるのは…？
そう、1＋1＋1＝3か、2＋2＋2＝6しかありません。
したがって、3桁のXが3の倍数になるのは、111と222の2通りです。

(2)
中学受験生にとっては、いろいろな解法が考えられます。
何なら、5回くらいであれば、すべて書きだして調べることも充分できますね。
ただ、(3)につなげるために、ここでは前回扱った考え方を生かすことにします。

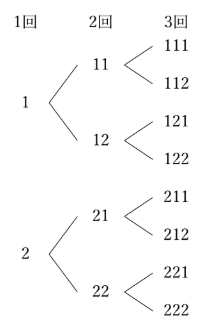
上の図は、硬貨を3回目まで投げたときにできるXの値を、樹形図に表したものです。
さて、「3で割り切れる」かどうかを考える応用問題では、「3で割った余り」に注目すると見通しが良くなることがあります。

そこで、上の樹形図に現れている数を「3で割った余り」に置きかえてみます。

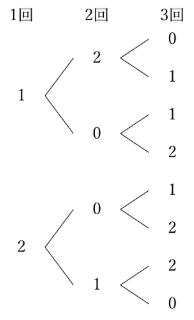
ずいぶんすっきりしましたね。
そして、これをよく観察すると…、

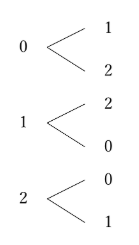
この3パターンの枝分かれだけが繰り返し現れています。
ということは…、

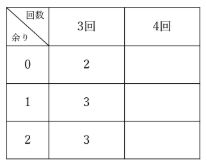
樹形図の3回目の枝には、0が2個、1が3個、2が3個書かれています。
そして、これらの枝が4回目に向かって枝分かれするときには、

0→1と2
1→2と0
2→0と1

このように分かれるので、

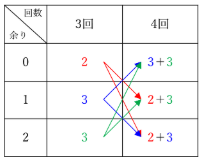
4回目に現れる0、1、2の個数はこのように計算できます。つまり、

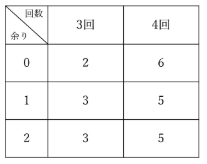
4回目の枝の本数も。この表のように求められました。
求めるのは5回投げたときですから、あと1回分、同じ計算をしましょう。

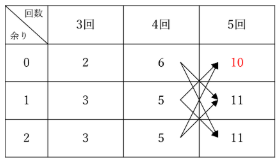
「3で割り切れる」とは余りが0になるということですから、(2)の答えは上の表に赤で示した10通りです。

(3)
同じように、8回投げたときの枝の本数を計算していけば良いのですが、(3)では「6で割り切れる」場合を問われています。
Xが6の倍数になるためには「3の倍数であり、しかも2の倍数」であれば良いですね。

Xが2の倍数になるためには、最後に投げたときに裏が出て、1の位に「2」が記録されなければいけません。
つまり、X＝□□□□□□□2、7つの□は1か2で、1の位だけは必ず2という形をしています。

ここで、7桁の□□□□□□□の部分は、どんな数であれば良いでしょうか。
Xは3の倍数でもあるので、数字の和である、□＋□＋□＋□＋□＋□＋□＋2が3の倍数であれば良いですね。
ということは、□＋□＋□＋□＋□＋□＋□の部分は3－2＝1より、「3で割った余りが1」になっているはずです。

これはつまり、「硬貨を7回投げたときには、3で割った余りが1」になっていて、「8回目には裏が出る」ということです！

(2)で書いた表の続きを、7回目まで書いてみます。

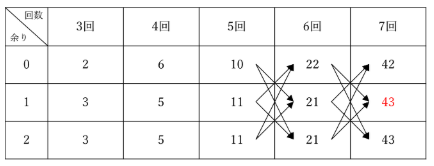
このようになりました。表に赤字で示したように、7回まで投げたときに「3で割った余りが1」になるＸは43通りあります。
このそれぞれの1の位に「2」を付け加えれば「8桁の6の倍数」になるので、答えは43通りと分かりました！

前回の東大の問題と同じように、直前の結果を利用して表にまとめることで、この問題も解決できました。
もともとの京大の問題には、もちろん数学で学習する手法を用いる必要がありますが、中学受験に向けた学習の中でこのような考え方に触れていると、元の問題を解く際にも方針が立ちやすくなります。

6年生は、この夏にも、似た考え方に触れる機会があるかもしれません。中学入試に向けて、そして少し未来の大学入試に向けても、意識して身に付けていきましょう。

今回はここまで。