こんにちは。算数を担当しています佐々木裕子です。

本日は、おうぎ形の中心が動いたあとの図形はほぼすべて同じ！ということをお伝え致します。
当たり前でもあるし、もうお気づきの方もたくさんいらっしゃると思いますが、
例題で説明していきます。

問題：下の図のように、中心角が60°で半径が6㎝のおうぎ形OABを、直線ℓに沿ってすべらないようにアの位置からイの位置まで転がしました。中心Oが動いたあとの線の長さは何㎝ですか。円周率は3.14とします。

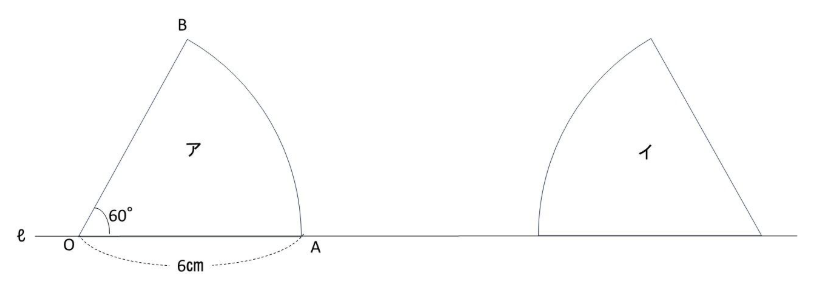
点Oは点Aを中心に半径6㎝で中心角90°のおうぎ形を描きます。
分かりにくい場合は、点Oだけ見て、点Oが点Aを中心に直線AOが直角に動き、点Aの真上に点Oが来ます。
その後、おうぎ形OABの弧ABが床に着きながら動くので、点Oは直線を描きます。
この理由は、床とおうぎ形の中心Oは必ず同じ半径の距離を保ちながら動くからです。
図の黄色い線は、おうぎ形OABの弧ABの長さと等しくなります。
最後に点Oは、イの状態になるとき、点Bを中心に半径6㎝で中心角が90°のおうぎ形の弧を描きます。完成した作図は下の図になります。

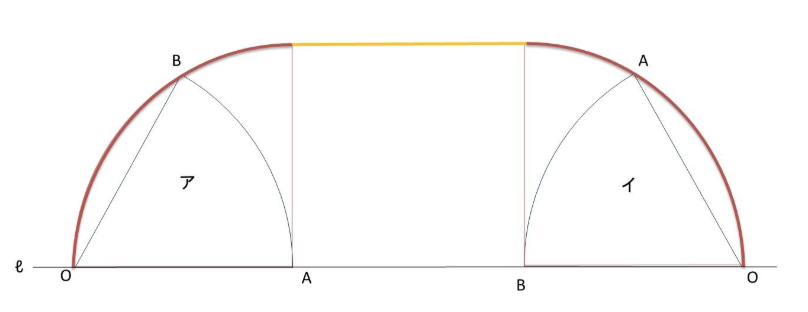
まとめると、
半径6㎝、中心角90°の弧が2つと、半径6㎝、中心角60°の弧を動いていきます。
6×2×3.14××2＋6×2×3.14×＝6×2×3.14×＝25.12㎝

では、他のおうぎ形も見てみましょう。

中心角150°で半径6㎝のおうぎ形OABを、直線ℓに沿って、中心Oが再び直線ℓ上にくるまで回転しました。点Oが描いた曲線の長さを求めなさい。

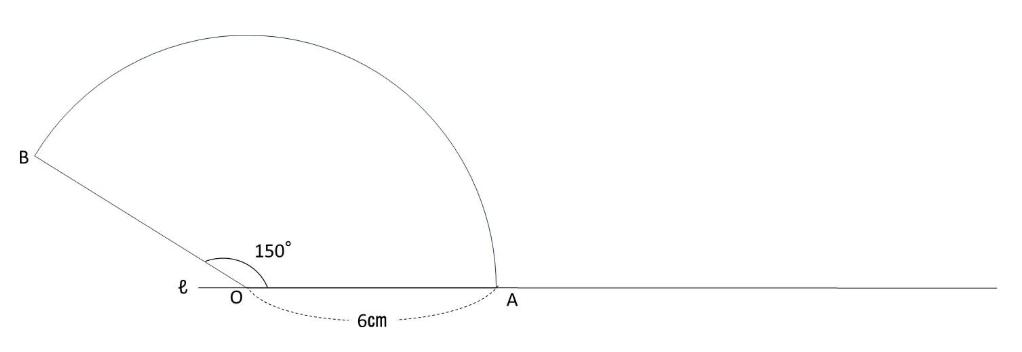
先ほどのおうぎ形より中心角が大きく、描く図が大変そうに思えますが、
実は、簡単です！

今日のポイントはここです！

点Oが描いた曲線は、実は先ほどの問題とほぼ同じ図形になるということです！

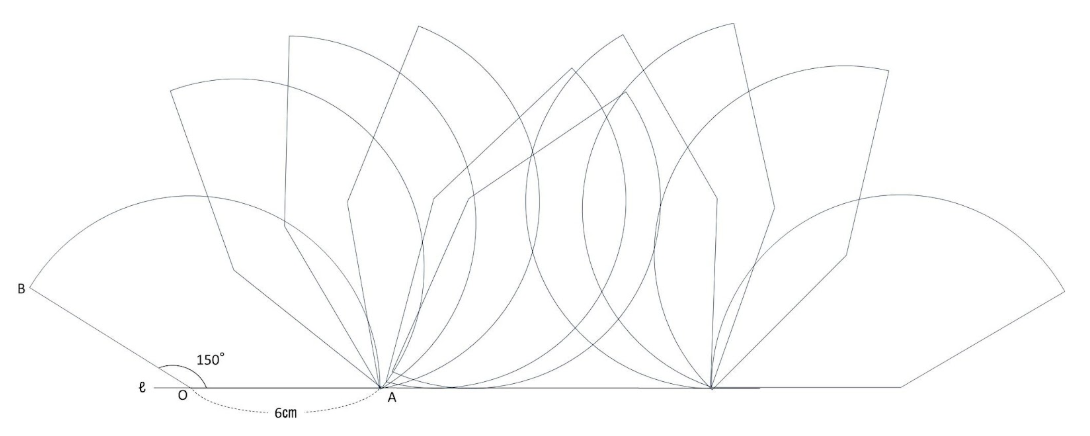
動いていく様子を細かく描いてみると、上の図のようになります。
やや複雑に見えますが、

点Oが描いた曲線は、下のようになります。

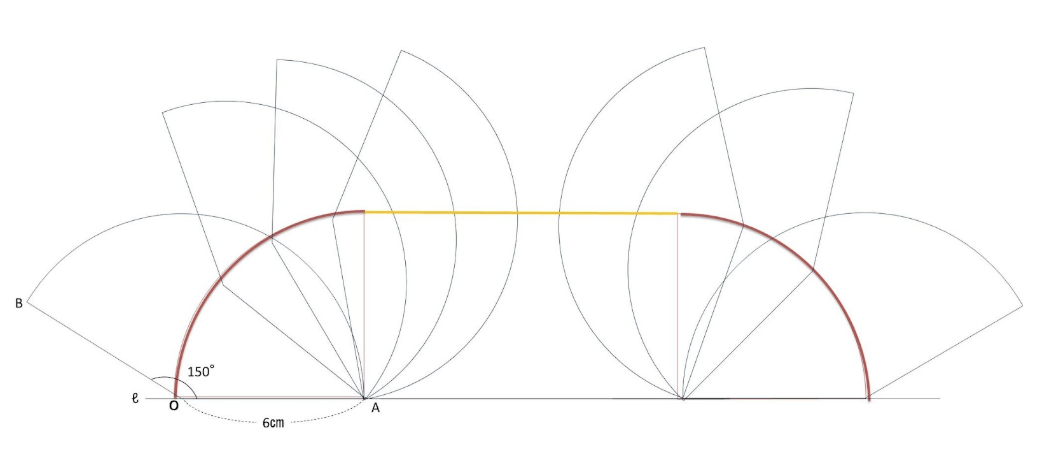
おうぎ形OABの図は、範囲が大きくて描きにくいですが、実は、点Oの動きは、
60°のおうぎ形とほぼ同じ動きをします。
弧の長さが違うので、黄色い部分の長さは異なりますが、90°のおうぎ形の弧の長さが2個分は変わりません。

おうぎ形の中心Oの動きは、中心角が変わっても、描かれた曲線はほぼ同じです。
よって、
6×2×3.14××2＋6×2×3.14×＝34.54㎝となります。

まとめると、

おうぎ形が直線ℓ上をすべらず回転して動くとき、中心Oの動きは、中心角が何度であろうと、
90°のおうぎ形の弧が2個分と、おうぎ形の中心角の弧の長さということになります。

です。

今度おうぎ形を回転させるという問題が出てきたときに、この考え方も思い出してみてください！