こんにちは。算数を担当している佐々木裕子です。

本日は、「解き方改革」についてお話いたします。

つまり、比を使って解いてみようねということです。

この夏、5年生の皆さんは「比」を習います。
そして、6年生の皆さんは、入試問題を解いていく時期になります。

指導していて思うのは、
「確かに、比を使わなくても解けるけど、比を使った方がいいよね」
という問題を、やはりずっと比を使わずに解いてしまっている生徒さんがいるということです。

例えば、

比を利用すると、面積図またはてんびん図というものを使います。

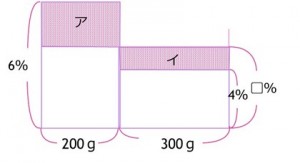
アとイの面積が等しいということに注目して、

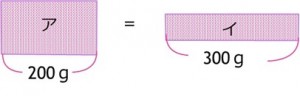
横の比が、　ア：イ＝200：300＝2：3
たての比は、面積が等しいので横の比、ア：イ＝③：②となります。

③＋②＝⑤が6―4＝2％にあたるので、
① ＝2÷⑤＝0.4％になります。
そうすると、②＝
0.4×2＝0.8で混ぜた後の濃度は、4＋0.8＝4.8％となります。

これを、もちろん食塩水の中にある食塩の重さを求めて解くこともできます。
0.06×200＋0.04×300＝12＋12＝24ｇ
24ｇ÷（300＋200）＝0.048となり
4.8%です。

このレベルであれば、もちろん食塩の重さを求めて解くこともできるのですが、
比を利用してしか解けない問題ができてきます。
そうすると、やはり、どうやって面積を描くのか、比をどこに利用するのかを練習しておかないと
解くことができません。

このような問題は、究極的ですが、
比でしか解けません。具体的な食塩水の重さがでていないにもかかわらず、
濃度を出さないといけないというときです。
先ほどの面積図を利用すると、

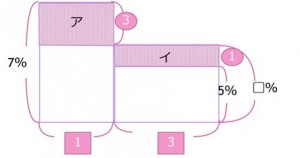
横の比が　ア：イ＝１：３
たての比が　ア：イ＝３：１となり、③＋①＝④が7－5＝2％になるので、
① ＝0.5%
よって、5＋0.5＝5.5%になります。

このように、究極ですが、比しか使えない問題もあります。
（1：3の量を適当に100g、300gというようにおいて解くこともできますが）

8月、9月にテストを受けたときに、
どの解き方で解いているのか、その部分をこちらで見ていきます。

答えは合っているからいいというのではなく、解き方を増やしていくということが、大切です。

「解き方改革」です！！

この夏に学んだ比を使えるようにしていきましょう。