こんにちは。受験ドクターの坂井です。
2月より新学年がスタートしました。
学習する量がふえて1か月が過ぎましたが慣れてきたでしょうか。

さて、今回は数え上げるのは少し大変だけどちょっとした発想を変えることで楽に集計できるものを1つ皆さんと考えていきたいと思います。

こんな問題です。見たことあるかな。

要は1～2022まで数字を書くときに2という数字を何回書いたかという問題です。

まず1～99について考えてみましょう。

1の位で2が使われるのは
2,12,22,32・・・82,92の10個。

10の位で2が使われるのは
20,21,22,23・・・28,29の10個

あわせて20個　　　と数えていくことでしょう。

ところが、ここでちょっと発想を変えて

こんな数え方はどうでしょう。
1～99までの中に出てくる2の個数と0～99までの中に出てくる2の個数は変わらないので0～99として数えていきます。

まず1の位に現れる2の個数について考えると

0～99までの100個の整数はすべてに1の位があります。（当たり前ですが。）その1の位に現れる数字は1だけ特別に多くあらわれることもなく、2だけ特別に多く現れることもありません。

0～9までの10種類の数字がみな平等に現れてきますよね。

だから0～99の整数で1の位に２という数字は　100÷10＝10個　現れます。

同じように考えると、10の位に現れる２の個数も100÷10＝10個です。

したがって、1の位に10個、10の位に10個現れるので合計20個となるわけです。

では、もっと範囲を広げて、1～999で考えてみましょう。
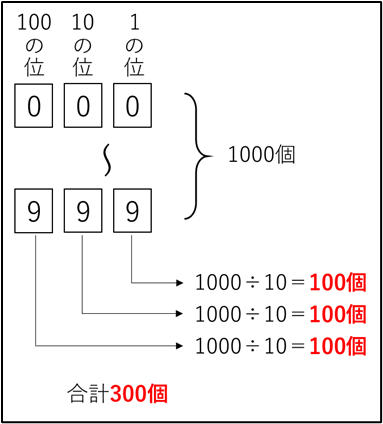
1の位、10の位、100の位のいずれも0～999までの整数1000個について0～9の10種類の数字が平等に現れるわけですから、２の数字が登場する回数は他の数字と同じです。

1の位：　1000÷10＝100個
10の位：　1000÷10＝100個
100の位：　1000÷10＝100個

合計300個　となります。

このように考えて、1～2022までについて解答してみましょう。

1～2022でも0～2022でも現れる２の数字の個数は変わらないので0～2022として考えます。

0～1999までと2000～2022までに分けて数えていきます。

①　0～1999までの2000個の整数の中で各位に何回(何個)２の数字が現れるのかを見ていきます。

1の位：　2000÷10＝200個
10の位：　2000÷10＝200個
100の位：　2000÷10＝200個
　　合計600個

②　2000～2022までの23個の整数の中で各位に何回(何個)２の数字が現れるのかを見ていきます。
　ここは計算ではなく丁寧に数えていく必要があります。

1の位：2002,2012,2022の3個
10の位：2020,2021,2022の3個
100の位：100の位に2は現れないので0個
1000の位：2000～2022の全てに出てくるので23個
　　合計29個

よって　600＋29＝629個　になります。

どうでしょう。だいぶ楽に数えられると思いませんか。
ぜひ、皆さんも試してみてください。

では、またお会いしましょう。