みなさん、こんにちは。
受験ドクター算数・理科科の川上と申します。
そろそろ新学年初めての大きなテスト、という子も多いのではないでしょうか。
全力でテストに取り組み最高の結果を出しましょう!
さて、本日は2021年入試の中から素数に関する問題に触れたいと思います。
2021=43×47
ということもあり、素因数分解、または素数の積に関する問題が複数の学校で出題されました。
それでは問題です。
次のように整数が並んでいます。
4,6,9,12,15,20,・・・
この数の並びの中の隣り合う2つの数について、左の数にその数を割り切る最も大きい素数を加えたものが右の数となっています。
例えば、隣り合う2つの数4と6について、左の数4に、4を割り切る最も大きい素数2を加えたものが右の数6です。また、隣り合う2つの数6と9について、左の数6に、最も大きい素数3を加えたものが右の数9です。[豊島岡女子、一部省略]
(1)15番目の数を答えなさい。
(2)この数の並びの中の数のうち、もっとも小さい47の倍数を答えなさい。
[解説]
(1)4,6,9,12,15,20,・・・
20の約数は1,2,4,5,10,20です。この中で最大の素数は5です。20の次の数は25になります。この要領で25以降も調べていくと
4,6,9,12,15,20,25,30,35,42,49,56,63,70,77,・・・
となります。よって15番目の数は77です。
(2)改めてこの数列の特徴について考えてみます。

数字の増え方が変わるところに〇をつけてみます。
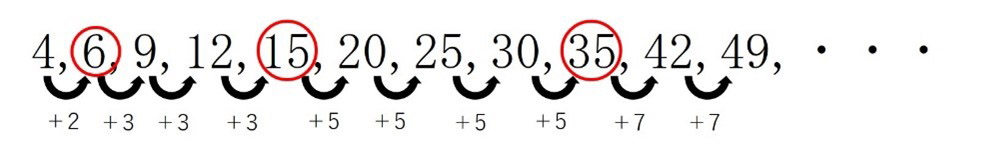
さて、この〇をつけた数字にはある規則があります。
気付きましたか?
今回のポイントは素数でした。素数は以下のように並びます。
2,3,5,7,11,13,17,19・・・
6 =2×3
15=3×5
35=5×7
そう、〇をつけたこれらの数字は、隣り合う2つの素数の積になっています。
また、はじめての5の倍数は15(=3×5)、はじめての7の倍数は35(=5×7)となっています。
構造に気付きましたか?
はじめての47の倍数は、47と、その一つ前の素数43との積になります。よって
43×47=2021
が答えとなります。
少し横道にそれますが「もしかしたら、2021の前に47の倍数があるのではないか」「本当に2021がはじめての47の倍数なのか」という疑問を抱く子もいるかもしれません。普段の学習の中でも「なぜ?」「どうして?」と考えることは極めて重要です。是非考えてみてください。
さて、来年は 2×3×337 = 2022年。どんな問題が出題されるのか、今から楽しみですね。
では、今回はここで失礼いたします。




