みなさん、こんにちは。
受験ドクターの坂井 智則です。

さあ、2月1日まで６０日を切りました。
残りの時間、志望校合格に向けて全力で頑張っていきましょう。
我々受験ドクターの講師陣もきみたちを全力でサポートしていきます！

今回は席替えの問題！
3人のうち2人が席を替わります。ただし、同じ2人が連続で席を替わることはできないとします。
このとき、席の替わり方は何通りあるのかというものです。

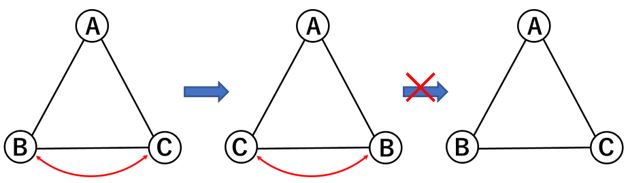
同じ2人が連続で席を替われないとは、次の図を例にするとBとCが席を替わった後に続けてBとCが席を替わることはできないということです。

どこに着目するところから考えていこうかと途方に暮れてしまいそうですが、実はもとに戻るためには席替えの回数を偶数回行わなければならないのです。
このことは、次に示す右回り・左回りに着目すると容易に理解することができます。

【着目点：その１】

左回り・右回りに着目する！

⇒　元の位置に戻るためには偶数回の席替えを行う！

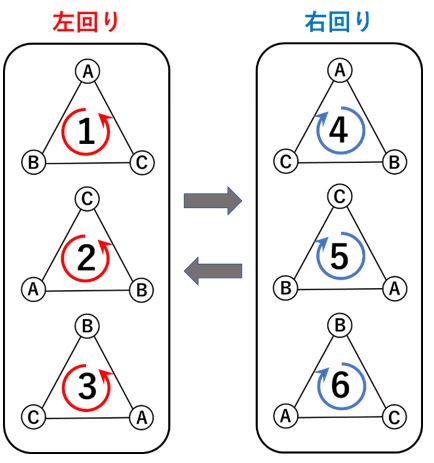
上の図で１がはじめの席だとすると元の位置は
ABC順番は左回りになっています。席替えを１回
行うと４か５か６のいずれかの位置になります。い
ずれも右回りの位置になります。さらにもう1回席
替えをするとまた左回りの位置になります。すなわ
ち、席替えを１回、3回、5回・・・・・と奇数回行うと
いずれも右回りの位置になり、元の位置には絶対
に戻ることができません。したがって、元の位置に
戻るためには、席替えを2回、４回、6回・・・・・偶
数回行う必要があることになります。
【着目点：その２】　２回席替えを行うと１２０度回転する！
上の図で1をスタートの位置とすると１回の席替えで4か5か6の位置になります。4からさらに１回席替えをすると同じ２人が連続で席替えすることができないことを考慮すると2か3の位置に戻ります。5からさらに１回席替えをしても6からさらに１回席替えをしても2か3の位置に戻ります。つまり、1の位置から２回席替えを行うと4、5、6のどの位置を経由しても2か3の位置になります。２回の席替えで1から2の位置に変わるということは反時計周りに120°、1から3の位置に変わるということは時計回りに120°回転することになります。

では、問題！
８回の席替え元の位置に戻るためには何通りの席替えの方法があるのか
を考えていきましょう。

着眼点その２の２回の席替えを「１ターン」ということにすると、８回の席替えで元の位置に戻るということは、
「４ターン」を行うということになります。

「４ターン」でもとの位置に戻るためには、反時計周りに120°と時計周りに120°をそれぞれ２回ずつ合計４回動くということになります。調べてみるとそれぞれが（ 0回，4回 ）や（ 1回，3回　）では元の位置にもどってこられません。
反時計周りに120°をA、時計周りに120°をBとするとAとBの順番はどうでもよいので、

① A　A　B　B
② A　B　A　B
③ A　B　B　A
④ B　A　A　B
⑤ B　A　B　A
⑥ B　B　A　A　　　　　　　　　の６通り。

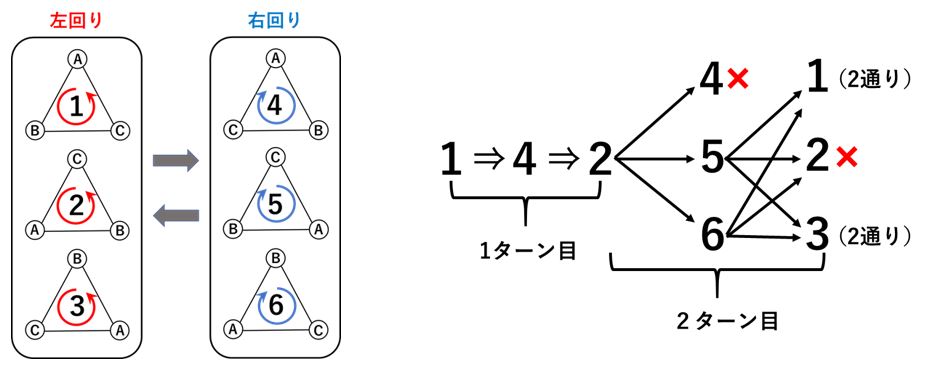
１ターン目にAの動きをするためには１から４または５、または６を経由して２になりますので３通り。同様に１ターン目にBの動きをする席替えの方法も３通りあります。つまり、１ターン目はAであろうがBであろう席替えの方法はどちらも　３通り　あることになります。
しかし、２ターン目は少し注意が必要です。

１ターン目を１⇒４⇒２と動いたとします。
同じ２人が連続して席替えをすることができないので２の次に４の位置になる席替えはできませんし、２の次は５か６になりますが、５の次に２の位置になる席替えもできません。

したがって、１ターン目が終わったとき２の位置にあり、その後２ターン目を終えて１に位置になる方法も３の位置になる方法も２通りになります。つまり、２ターン目以降は、AであろうがBであろうが席替えの方法は２通りあることになります。
以上より、A，Bの順番の決め方が６通り、１ターン目は３通り、２ターン目、３ターン目、４ターン目はいずれも２通りあるので、　８回の席替えで元の位置に戻る方法は、

６×３×２×２×２＝１４４通り　　　になります。

それでは、みなさん
またお会いしましょう。