みなさま、こんにちは。
受験ドクター算数科のHH講師です。

本日は、正方形の中にある正方形の問題を扱いたいと思います。

第1問

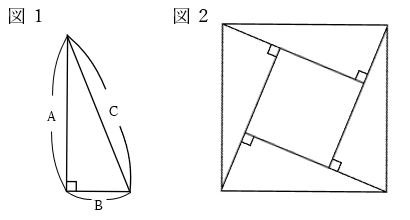
直角をはさむ2つの辺の長さの和が17㎝の直角三角形(図1)の紙が4枚あります。
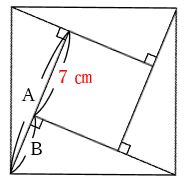
この4枚の紙を図2のようにならべると、大きい正方形と小さい正方形ができます。
このとき、真ん中にできた小さい正方形の面積は49㎠になりました。
これについて、次の各問に答えなさい。

（１）図1の直角三角形のAとBの長さはそれぞれ何㎝ですか。
（２）大きい正方形の面積はいくつですか。
（３）図1のCの長さは何㎝ですか。

以下、解説です。

（１）解説

真ん中の正方形は、その面積が49㎠という条件から、1辺が7㎝であることがわかります。このことから、AとBの長さの和が17㎝、AとBの長さの差が7㎝となります。
よって、Bの長さは(17-7)÷2＝5㎝、Aの長さは5+7＝12㎝です。
A　12㎝
B　 5㎝

（２）解説

（１）より、AとBの長さがそれぞれ12㎝と7㎝となりましたので、直角三角形の面積は
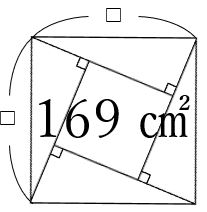
12×5÷2＝30㎠となります。大きな正方形の面積は、直角三角形の紙4枚分と真ん中の小さな正方形の和で求まるので、30×4+49＝169㎠です。
大きい正方形　169㎠

（３）解説

（２）より、大きい正方形の面積が169㎠となりましたので、その1辺の長さを考えます。
□×□＝169を満たす数は、13です。
C　13㎝

このように、正方形の中にある正方形の問題は、直角三角形の辺の長さに着目し、直角をはさむAとBの長さの和やAとBの長さの差を利用することがポイントです。

ここからは少し難しい問題2題をご紹介します。

第2問

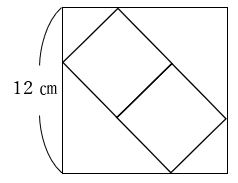
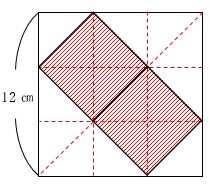
下の図のように、1辺12㎝の正方形の中に、大きさの等しい小さい正方形が2つ入っています。小さい正方形2つ分の面積の和を求めなさい。

この問題は、2つの解法を紹介します。

以下、解説です。

【パターン①分割して考える】

上の図のように、同じ大きさの直角二等辺三角形に分けると、赤い影の部分の面積は全体のです。
よって、小さな正方形2つ分の面積は12×12×＝64㎠です。

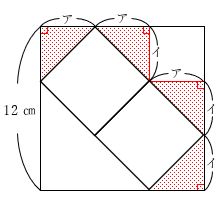
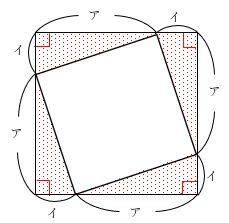
【パターン②直角三角形の2辺の和を考える】

上の図の赤い影のついた4つの直角三角形は斜辺の長さが等しいので、合同です。
図より、アの長さが3つ集まると12㎝ですから、アの長さは12÷3＝4㎝です。
同様に、イの長さが3つ集まると12㎝ですから、イの長さは12÷3＝4㎝です。
アとイの長さが等しいので、赤い影のついた三角形は直角二等辺三角形になることが分かります。
この後の解法は様々ありますが、小さい正方形は赤い影のついた直角二等辺三角形の面積の4倍となるので、小さい正方形2つ分の面積は4×4÷2×4×2＝64㎠です。
小さい正方形2つ分の面積　64㎠

第3問(難)
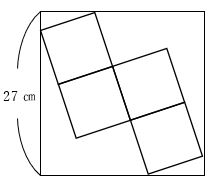
1辺27㎝の正方形の中に下のように、大きさの等しい小さい正方形が4つ入っています。小さい正方形4つの面積の和を求めなさい。

以下、解説です。

解説

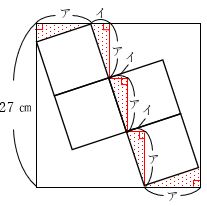
上の図のように、影のついた合同な直角三角形に着目します。
アの長さが3つ集まると27㎝になりますので、アの長さは27÷3＝9㎝です。
アの長さ2つ分とイの長さ3つ分が集まると27㎝になりますので、ア×2+イ×3＝27より、9×2+イ×3＝27㎝、イ×3＝9㎝、イの長さは3㎝です。
下の図を参考に、小さな正方形1つ分の面積を求めます。

小さい正方形を合同な直角三角形で囲みます。
ア＝9㎝、イ＝3㎝より、全体の面積は12×12＝144㎠です。
直角三角形1つ分の面積は3×9÷2＝13.5㎠です。
このことから、小さい正方形の面積は144-13.5×4＝90㎠です。
よって、求める面積(小さい正方形4つ分)は90×4＝360㎠です。

いかがでしたでしょうか？
最後の問題はなかなか解き応えがあったのではないでしょうか？
いずれの問題も、直角三角形の辺の長さの和や差に着目するとことで解ける問題でした。
受験算数は着眼のポイントがわかっていないと解けない、もしくは、解くことに時間がかかるものです。
「正方形の中にある正方形の問題は、直角三角形の辺の和や差に着目する」というポイントを思い出し、似たような問題が出たときの有効な手立てとなるか実践してみてください。

では次回、またお会いしましょう。