みなさん、こんにちは。受験Dr.の桑田陽一です。
9月の講師ブログをお届けします。

今回は、2025年2月25日に行われた京都大学の入学試験から前回に続いてもう1題紹介します。
前回は文系学部の問題でしたが、今回は理系学部を目指す受験生が取り組む数学の問題です！

問題

正の整数x、y、zを用いて

N＝9z^2＝x^6＋y^4

と表される正の整数Nの最小値を求めよ。

(2025京都大学　理系　大問2)

「z^2」という記号は見たことがない人が多いでしょう。
「zを2個かけ合わせた数」、つまり「ｚ×z」のことを表します。
同じように、「x^6」は「xを6個かけ合わせた数」、「x×x×x×x×x×x」のことを表し、「y^4」は「y×y×y×y」のことを表しています。

アルファベットの「x」と、掛け算の記号の「×」が入り交じって分かりにくいので、問題の内容を変えずに中学受験生向けの表現に書き換えてみます。

問題(改)

0より大きい3つの整数A、B、Cを使って、

　N＝9×A×A＝B×B×B×B×B×B＋C×C×C×C

と表すことができる整数Nのうち、最も小さいものを求めなさい。

これで、中学受験生も問題の意味が理解できるようになったでしょう。
意欲のある受験生ならこのままでも解けないことはないのですが、実のところ、これは優秀な高校生にとってもかなりの難問。
中学受験生もステップを踏んで考えられるように、小問を加えます。
一緒に考えていきましょう。

(1)
Pを3で割り切れる整数、Qを3で割ると1あまる整数、Rを3で割ると2あまる整数とします。
P×P、Q×Q、R×Rを3で割った余りはそれぞれいくつになりますか。

－－－－－

P×Pについては易しいはずです。
Pは3の倍数ですから、P×Pも3の倍数。したがって3で割った余りは0ですね。

では、Q×Qはどうでしょうか。

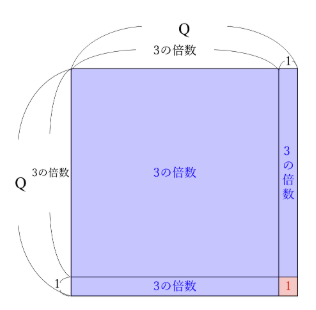
Qは3で割ると1あまる整数なので、Q×Qは上の図で示した正方形の面積と考えることができます。
ここで、図の青い部分は3の倍数になっているので、この正方形の面積を3で割ったときの余りは、右下の赤い部分、つまり1であることが分かります。

同じように3で割ると2あまる整数をRとしたときは、

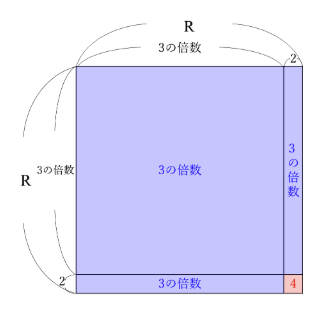
こんな図で表すことができ、これを3で割った余りは、右下の部分の4を3で割った余り、すなわち1になります。

まとめると、

3で割り切れる整数をPとすると、P×Pを3で割った余りは0、
3で割ると1あまる整数をQとすると、Q×Qを3で割った余りは1、
3で割ると2あまる整数をRとすると、R×Rを3で割った余りは1、

と分かりました。

(2)
A、B、Cを0より大きな整数としたとき、
9×A×A＝B×B×B×B×B×B＋C×C×C×C
という式について、以下の文の空欄に当てはまる数を求めなさい。

9×A×Aを3で割ったときの余りは(　①　)です。

B×B×B×B×B×Bを3で割ったときの余りは、
Bが3で割り切れる整数のとき(　②　)、
Bが3で割ると1あまる整数のとき(　③　)、
Bが3で割ると2あまる整数のとき(　④　)です。

C×C×C×Cを3で割ったときの余りは、
Cが3で割り切れる整数のとき(　⑤　)、
Cが3で割ると1あまる整数のとき(　⑥　)、
Cが3で割ると2あまる整数のとき(　⑦　)です。

したがって、Bを3で割ったときの余りは(　⑧　)、Cを3で割ったときの余りは(　⑨　)です。

－－－－－

9×A×Aは明らかに3で割り切れます。したがって、①は0です。

B×B×B×B×B×Bについて、
Bが3で割り切れる整数であれば、B×B×B×B×B×Bも明らかに3で割り切れます。したがって、②も0。
Bが3で割り切れないときは、 (1)で見たように余りの部分のみに注目すれば、積を3で割ったときの余りも分かります。
③は、余りの1に注目し、1×1×1×1×1×1＝1を3で割ったときの余り、すなわち1です。
④は、余りの2に注目し、2×2×2×2×2×2＝64を3で割ったときの余り、すなわち1です。

同じように考えれば、C×C×C×Cについても、3で割ったときの余りは、
Cが3で割り切れる整数のとき0…⑤、
Cが3で割ると1あまる整数のとき1…⑥、
Cが3で割ると2あまる整数のとき1…⑦
であることが分かります。

以上のことをまとめると、B×B×B×B×B×BもC×C×C×Cも、
BやCが3の倍数であれば3で割り切れ、BやCが3の倍数でなければ3で割ると1あまるということになります。

さて、そこで、
9×A×A＝B×B×B×B×B×B＋C×C×C×C
という式について、少し考えてみましょう。

左側の9×A×Aは3の倍数です。
右側にあるB×B×B×B×B×BもC×C×C×Cも、3の倍数であるか、または3で割ると1あまる整数です。
これらを足し合わせて3の倍数になるのは、B×B×B×B×B×BとC×C×C×Cの両方とも3の倍数である場合しかあり得ません。

つまり、BもCも3の倍数であり、空欄の⑧と⑨に当てはまる数はいずれも0です。

－－－－－

ここまでをまとめると、

0より大きい3つの整数A、B、Cを使って、

N＝9×A×A＝B×B×B×B×B×B＋C×C×C×C

と表すことができるとき、「BもCも3の倍数である」ということが分かりました。

これを踏まえて、あと2ステップ考えてみましょう。

(3)
以下の文の空欄に当てはまる、最も大きい整数を答えなさい。

0より大きい3つの整数A、B、Cを使って、

N＝9×A×A＝B×B×B×B×B×B＋C×C×C×C

と表すことができるとき、
(2)より、B×B×B×B×B×Bは必ず(　①　)の倍数であり、C×C×C×Cは必ず(　②　)の倍数です。

(4)
0より大きい3つの整数A、B、Cを使って、

N＝9×A×A＝B×B×B×B×B×B＋C×C×C×C

と表すことができる整数Nのうち、最も小さいものを求めなさい。

－－－－－

「BもCも3の倍数である」ということをヒントに、(3)(4)を考えてみてください。
ずいぶん長くなったので、今回はいったんここまで。

次回、解決編をお送りします。