みなさんこんにちは。

受験ドクターの桑田陽一です。

 

夏休みもいよいよ残すところ1週間ですね。

5年生は、この夏休みに初めて比を習ったという人もたくさんいるはずです。

皆さんが比を習いたてであるこの時期、今回は「比例感覚」についてお話しします。

4年生以下にも6年生にも役に立つ部分があると思いますので、参考にしてくださいね。

 

さて、「比例感覚」とは？受験算数(そして理科)を良い形で学んでいくために、大変重要な感覚です。

今回も、簡単な例題を通してお話ししていきます。

 

例題1

次の□にあてはまる数を求めなさい。

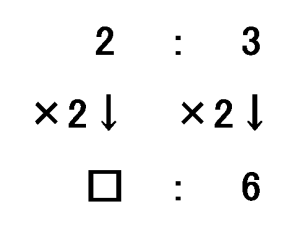
2:3=□:6

 

この問題で与えられているような、2つの比が等しいことを表す式を「比例式」と言いました。

比を習っていれば、これは簡単だという人が多いでしょう。正解は4です。

 

正解できましたか？しかし、正解できたからといって安心してはいけません。

正解を得るために、頭の中でどのような動きをしたでしょうか？

 

「外項の積＝内項の積」を使って、2×6＝3×□から求めた人がいたとすると、ほんの少しだけ心配になります。もしかして、機械的な解法暗記に走っていないかな？と…。

 

比例とは、「xが2倍、3倍…になると、yも2倍、3倍…になる」ような関係のことでした。

比例式の問題では、2つの比を縦に並べたようなイメージを持って、それぞれが何倍になっているかに注目するのが「比例感覚」を持った思考です。上の例では、後項が3→6と2倍になっていますから、前項も2倍になっているはずで、□＝2×2＝4と求めます。

 

非常に単純な例ですが、このように「比例関係」にこだわっていくことが、受験算数を極めるコツなのです。

 

例題2

はるかさんは、12分で900m歩きました。はるかさんの時速を求めなさい。

 

比ではなくて、速さの問題ですね。

あまり難しくはないはずです。速さ＝道のり÷時間ですから、900m÷12分から求めても良いのですが…。

 

今回求めたい「時速」とは、「1時間で進む道のり」のことですね。

「12分で進む道のり」が900mと与えられていて、1時間は60分ですから12分の5倍です。ということは…。

こんな関係になっていて、900m×5＝4500m=4.5kmより、時速4.5kmと求めることができます。

 

実は、前回の「公式を覚えるな？」でも、速さを題材にさりげなく「比例感覚」に触れていました。公式を「腑に落とす」ためにも、「比例感覚」は重要です。

 

例題3

5%の食塩水300gに含まれる食塩の量は何gですか。

 

今度は、割合の論点の1つ、食塩水の問題ですね。

こちらも基本的です。正解は15g。合っていましたよね？

 

さて、どう考えたでしょうか？

300g×0.05=15gという式を立てたみなさん、決して悪くありません。ほとんどの人がそう求めることでしょう。

 

「比例感覚」で考えるとどうなるの？と思ってくれた人、ありがとう。嬉しいです。

 

5%とは、「100分の5」。

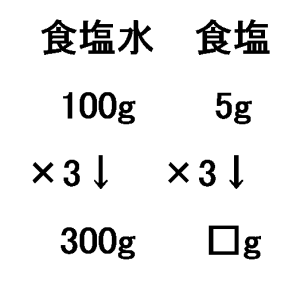
すなわち「食塩水100gあたり5gが食塩」だということです。そんな割合で食塩を含むような食塩水が300gあるということは…。

食塩水全体の重さが、100g→300gと3倍になっているので、食塩の量も3倍になっているはず。すなわち、食塩の重さは、5g×3＝15gと求まります。

 

えー、ちょっと不自然じゃない？と思いましたか？

しかし、私の経験上、受験算数が本当に得意な子は、複雑な問題を解きほぐしていく過程で、一つ一つの数値を求めるときには、こんな思考であることが多いのです。

 

また、「比例感覚」は算数のみならず、理科の計算問題、特に化学の各分野でも、計算の省力化に強烈な効果をもたらします。機会を改めて、具体的に紹介します。

 

さて、基本的な問題3つのみの短い記事でしたが、読んでみて、思考が良い方向に変わった気がする人がきっといるはずです。

 

そんな人は、ぜひ今後の勉強で「比例感覚」にこだわってみてください。算数の問題を解くときの見通しが、必ずや晴れてくるはずです。