みなさん、こんにちは。
受験ドクター算数・理科科の川上と申します。
毎月模試があり、過去問も解き、塾の宿題もこなして・・・
受験生の皆さんの頑張りには本当に頭が下がります。
ここからが正念場です。
体調に気を付けて、1日1日を大切に過ごしてほしいと思います。
さて、本日は立体の求積の問題の解法について触れたいと思います。
基本的な切断のルールはわかるけど、難しめの問題になると解けなくなってしまう、そんなお子さまの助けになればと思います。
やや難解な問題かもしれませんが、是非最後までお付き合いください。
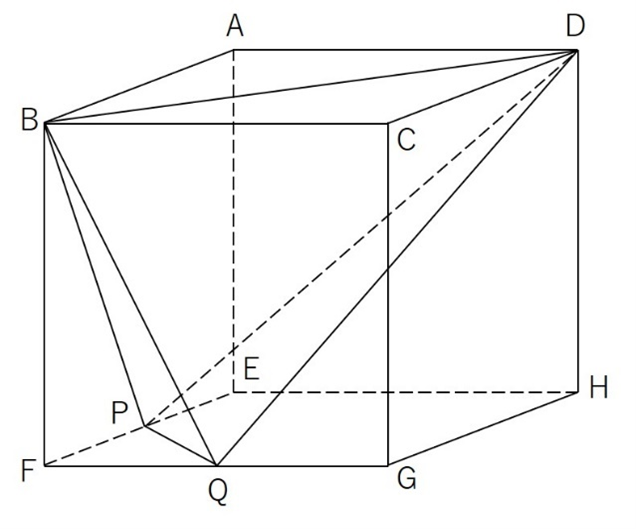
いかがでしょうか。
類似の問題として以下のような正四面体BDEGの求積の問題なら解いた経験があるかもしれません。
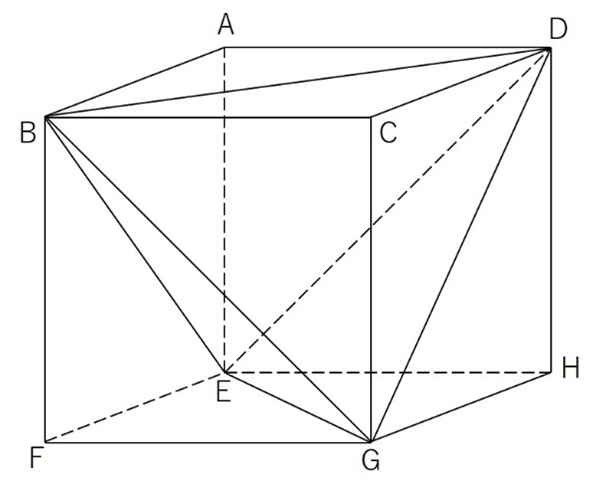
これなら三角すいを4つ引けばすぐ体積を出せそうですが、今回の問題では全体から引く方法はかなり難しそうです。
【解説】
四面体BPQDの求積のために、隣接する三角すいBPFQを活用します。
この二つの立体は三角形BPQ(下の図の赤い三角形)を共有しています。
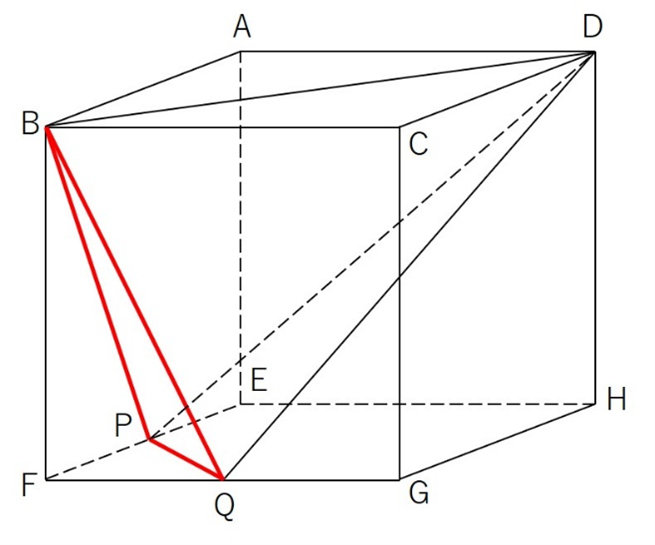
勘の鋭い子はもう気付いたかもしれませんね。
この赤い面を、四面体BPQDと三角錐BPFQの底面とみなします。
すると、それぞれの立体の高さは、下の図の青線で表される線分の長さとなります。
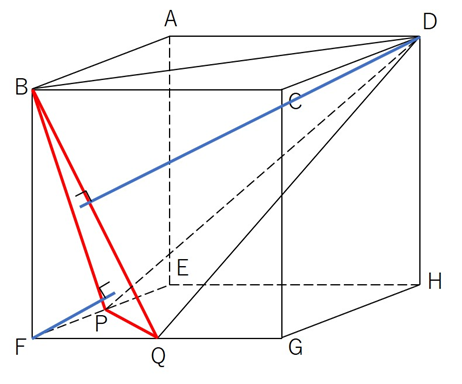
四面体BPQDと三角錐BPFQの底面は三角形BPQですので、この青い線の長さの比が、そのまま四面体BPQDと三角すいBPFQの体積比となります。
さて、方針がはっきりしました。このまま立体で考えてもいいですが、下の図の緑色の平面BFHDを切り取って考えてみます。
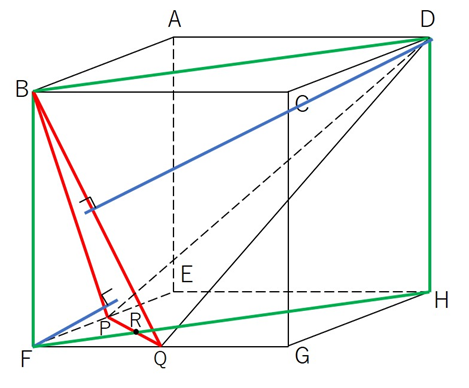
切り取ったのが下の図です。
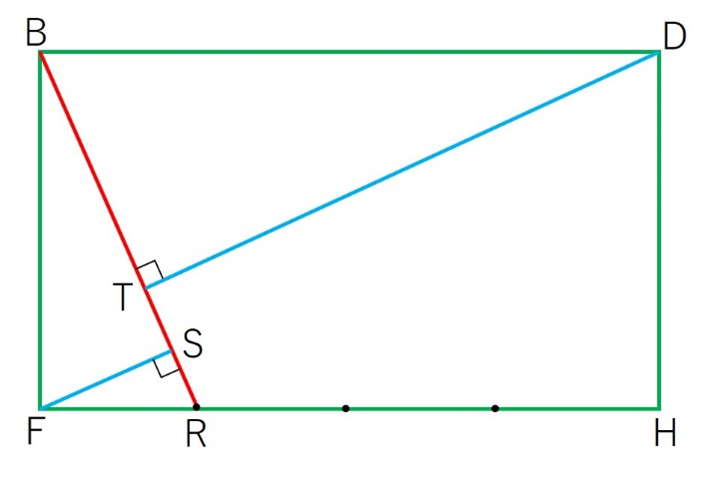
FHとPQの交点をR、FとDからBRに降ろした垂線とBRとの交点をそれぞれS、Tとします。
※さりげなく等分点をうっていますが、FR:RH=1:3です。底面は下の図のようになっています。
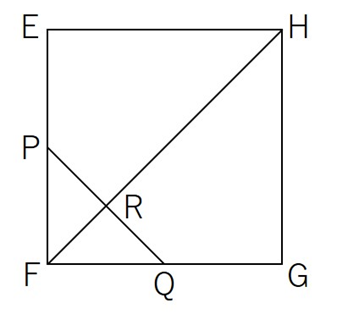
以下のように補助線を追加すれば納得しやすいかもしれません。
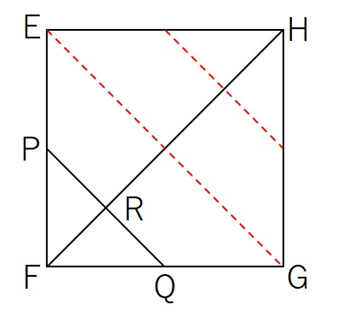
さあ、あと一息です。
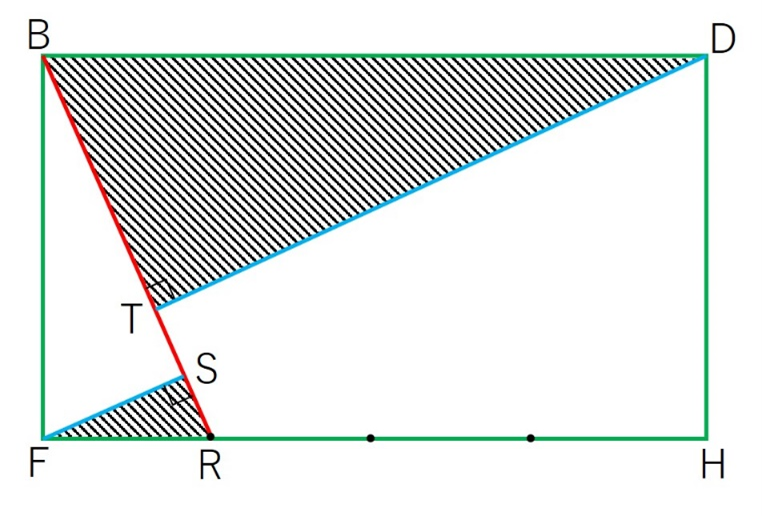
斜線部分の三角形BTDと三角形RSFは相似になっていて、相似比は4:1です。
つまり、TD:SF=4:1となります。
よって、四面体BPQDの体積は、三角すいBPFQの4倍です。
三角すいBPFQの体積は
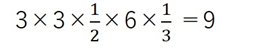
となるので、四面体BPQDの体積は
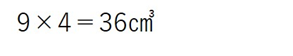
となります。
いかがだったでしょうか。
ちなみに私がこの問題をはじめて解いたときは、全体から三角すい1つと四角すい2つと五角すい1つを引きました。大変でした(涙)
ですので、この解法を知ったときは心の底から驚きましたし、非常にスッキリしました。
皆さんも、使えるタイミングを見極めてこの解法を活用してください。
また、ほかにも解法はいくつかあります。次回以降ご紹介できればと思います。




