こんにちは、受験ドクターのK.Dです！
6年生の方は受験当日まで3ヶ月を切りましたね。
今回は、「円すいの側面積」を一瞬で求める方法を確認しておきましょう。
今回みなさんと共有したいことは、いかに問題を解くうえで時間短縮ができるかです。

では、次の問題を解いてみてください。

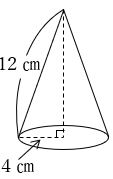
問　下の図の円すいの側面積を求めなさい。ただし、円周率は3.14とします。

いかがでしょうか。では、答えです。
一瞬で解く方法も載せているので最後まで読んでくださいね！

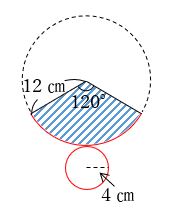
まずこの円すいの展開図を考えましょう。

すると上図のようになります。このとき120°以外の部分は
お分かりいただけると思います。
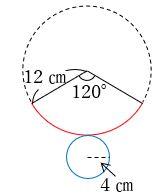
では、どうして120°になるのかを説明します。
上図で半径12㎝の円の弧の長さ（赤い部分）は円すいの底面の
周りの長さと同じになります。
つまり赤い部分の長さは8×3.14になると分かります。
半径12㎝の円の円周の長さは24×3.14なので、ちょうど3分の1になっています。
よって、360°の円の3分の1なので、120°と分かります。
あとは側面積である青斜線部の面積を求めればよいので、
12×12××3.14＝150.72㎠
となります。

次に一瞬で解く方法を説明するのですが、少しだけ寄り道をします。

側面積を求める式は12×12××3.14なのですが、
× の部分に着目してみたいと思います。

12×2×3.14× ＝ 4×2×3.14

を□とし、この式を簡単にすると、
24×□×3.14 ＝ 8×3.14
となります。つまり、□＝ と分かります。
実はこのように、この問題では中心角を求める必要性はなかったのです。
上記の等式から分かるように、□の部分は全てで求められるのです。

から2×3.14を相殺すれば
と同じですよね。

つまり、12×12××3.14は12×12××3.14と書き換えることができます。

すると、12×12××3.14となります。
つまり、12×4×3.14となります。
さあ、お気づきでしょうか。

母線×底面の半径×3.14になっていますね。
このように円すいの側面積は、

母線×底面の半径×円周率（3.14）

で求められます。
この方法を知っていれば相当時間短縮ができるので、知らなかった人、
知っていたけれど、忘れていた人は今回で覚えてしまいましょう。

この公式を知っていれば、こんな問題も一瞬で解けます！

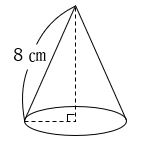
問　下の図の円すいの側面積は50.24㎠です。この円すいの底面の半径を求めなさい。
ただし、円周率は3.14とします。

では、早速答えです。
先ほどの公式に当てはめてみましょう。
母線×底面の半径×円周率（3.14）＝側面積
8×底面の半径×3.14＝50.24となるので、
底面の半径は、2㎝と分かります。

次回も受験までに確認しておきたい問題を紹介するので是非ご覧ください。