みなさん、こんにちは。
受験ドクター算数科の江田です。

今回は
「回転体」についてのお話。

その中でも
“小さな正方形”の集まりを回転させてできる立体の体積
についてです。

さっそくですが、
以下のような問題を考えてみましょう。
6年生のお子様をお持ちの方は、
是非お子様にチャレンジさせてみてください。

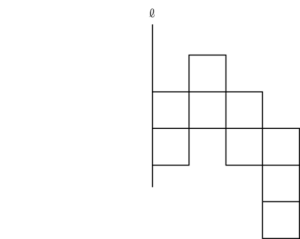
解答目標時間は2分以内！

いかがでしょう。

いくつか考え方があります。
このような問題に解き慣れている人は
「体積なら、この部分の正方形はこっちに移動しても変わらないから…」
というように、もともとの正方形の一部を移動して考えていこうとしたかも知れません。

ただ、この問題は正方形を移動したとしても
結局少し面倒なかたちになってしまったことでしょう。

もちろん、
回転させてできる実際の立体そのまま考えるよりはだいぶ楽になるとは思いますが…。

さて、今回のブログでお伝えしたい考え方は
「比を活用する」というものです。

たとえば以下の図のような
3つの正方形㋐～㋒が直線ℓを軸に1回転したときにできる立体
の体積を考えてみます。

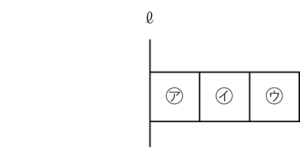
これら3つの正方形を1回転させたときにできる立体は
下の図のようになります。

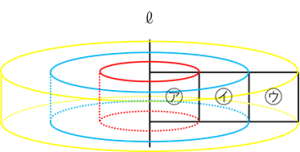
㋐を1回転させてできるのが赤の円柱。
㋐と㋑の2つを1回転させてできるのが青の円柱。
㋐と㋑と㋒の3つを1回転させてできるのが黄の円柱。

それぞれの円柱は「高さ一定」の円柱ですから
それぞれの「体積の比は底面積の比」となります。

ここで、それぞれの円柱の底面について考えます。
もちろん、それぞれの底面は「円」ですから「相似な図形」と言えます。
相似比(半径の比)は1：2：3なので、
面積比は(1×1)：(2×2)：(3×3)＝1：4：9
とわかりますね。

よって、それぞれの円柱の体積の比も1：4：9となります。
つまり、
㋐の正方形が1回転してできる立体
㋑の正方形が1回転してできる立体
㋒の正方形が1回転してできる立体
の体積の比は
1：(4－1)：(9－4)＝1：3：5
と求められます。

同じように考えると、
㋐、㋑、㋒よりもさらに外側に正方形がついた場合、
それぞれの正方形が1回転してできる立体の体積の比は

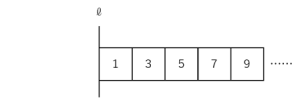
となっていきます。

この考え方を今回の例題に活用しましょう。
すると、それぞれの正方形が1回転してできる立体の体積比は

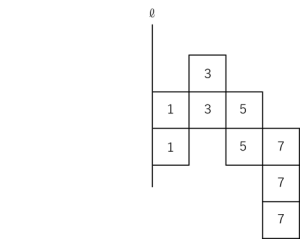
となります。
よって、この図の「１」の体積を求め、それを
1×2＋3×2＋5×2＋7×3＝39（倍）
すればよいことになります。

比の「１」の体積は
2×2×3.14×2＝8×3.14（㎤）
ですから、求める体積は
8×3.14×39＝312×3.14
　　　　　　　 ＝979.68（㎤）
と求められます。

いかがでしたか。
このような
“小さな正方形”の集まりを1回転させてできる回転体の問題においては、
是非今回の比の考え方を活用していきたいですね！

今回はここまで。
また次回のブログでお会いしましょう。