みなさん、こんにちは。
受験ドクター算数科の江田です。

夏休みも終わり、
6年生はいよいよ受験モード
といったところでしょうか。

入試本番までおよそ4か月。
1日1日を大切に過ごし、
第一志望校合格を勝ち取りましょう！

さて、前回のブログの最後に
次のような問題を出しましたね。

【問題】
財布の中に
100円玉が3枚
50円玉が3枚
10円玉が3枚
入っています。

これらの硬貨を使い、“支払うことのできる金額”は全部で何通りですか。
ただし、「0円」は含みません。

どうでしょうか。
答えは出せましたか？

前回のブログで、
このような問題は
『各硬貨をそれぞれ何枚使って支払うか』
がポイントとなることをお伝えしましたね。

このことを素直に実践してくださった方は
おそらく答えが
63通り
となりませんでしたか？

この答えになった方、
残念ながら不正解でした。

では、
なぜ前回の考え方をそのまま使ったら
不正解になってしまったのか。

その原因を探っていきましょう。
前回の考え方はこうです。

まず
『100円玉を何枚使うか』
の選択肢は、全部で

次に
『 50円玉を何枚使うか』
の選択肢は、全部で

そして
『 10円玉を何枚使うか』
の選択肢は、全部で

と考え、
これらを組み合わせて“支払うことのできる金額”は全部で
4×4×4＝64 （通り）
となりますが、ここには
“100円玉，50円玉，10円玉どれも1枚も使わない”
すなわち 「0円支払う」 が含まれてしまうので、
答えは
64－1＝63 (通り)
としましたね。

ここで皆さんに考えていただきたいことが。
これ、本当に
“支払うことのできる金額”
の場合の数になっていますか？

そもそも、今やってきた考え方は
『各硬貨をそれぞれ何枚使って支払うか』
だったんですよね。

たとえばこの中には
『100円玉を1枚，50円玉を2枚，10円玉を1枚』で支払う210円
と
『100円玉を2枚，50円玉を0枚，10円玉を1枚』で支払う210円
がどちらも含まれてしまっていますね！

他にも
『100円玉を1枚，50円玉を0枚，10円玉を2枚』で支払う120円
と
『100円玉を0枚，50円玉を2枚，10円玉を2枚』で支払う120円
など…。

そうなんです。
この考え方だと
100円玉と50円玉のあいだで
「枚数の組み合わせは異なっても、“支払う金額”は同じ」
になってしまうといった
ダブりが発生してしまうんです。

前回のブログで最初に出題した問題は
100円玉が3枚
50円玉が1枚
10円玉が2枚
という設定だったので、
「どのように枚数を組み合わせても、同じ金額にはならない」
状況だったのです。
このような場合には
素直に前回の考え方を使えばよい
ということだったのです。

では、
このタイプはどのように考えていくのでしょう。

それは、
「ダブりが発生しないようにうまく両替え」
してから考えればいいんです！

この
「うまく」
というところもポイントです。

具体的には以下のポイントに注意して両替えをしていきましょう。
① ダブりが出ないようにする
② もともとは払えた金額が払えなくなってはダメ
③ もともとは払えなかった金額が払えるようになってはダメ
以上3点です。

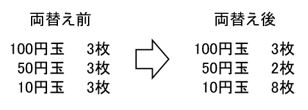
たとえば今回の問題を
次の 【例1】 のように
50円玉１枚だけ10円玉に両替えするのはどうでしょうか。

【例1】

どうですか？
これ…

かなり悪い例です！Σ(￣ロ￣lll)
なぜなら、注意すべき点①と③の
ダブりは相変わらず出るわ、
もともとは払えなかった金額（たとえば40円とか90円とか）が払えるようになるわ、
もう散々です！

どうです？
なんとなくつかめましたか？

それでは
正しい両替えを確認してみましょう。

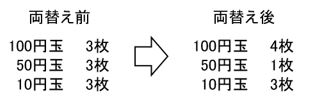
それは以下の 【例2】 のような両替えです。

【例2】

50円玉2枚を100円玉に両替えしたんです。
すると、50円玉が1枚になってくれたおかげで、
100円玉と50円玉のあいだでのダブりが発生しなくなったんです♪

また、
もともと払えた金額が払えなくなったりもしていませんし、
もともと払えなかった金額が払えるようになったりもしていません。
よって、この両替えをした後なら
前回の考え方を使えます！

すると、
『100円玉を何枚使うか』
の選択肢は、全部で

次に
『 50円玉を何枚使うか』
の選択肢は、全部で

そして
『 10円玉を何枚使うか』
の選択肢は、全部で

と考え、
これらを組み合わせて“支払うことのできる金額”は全部で
5×2×4＝40 （通り）
となりますが、ここには
“100円玉，50円玉，10円玉どれも1枚も使わない”
すなわち 「0円支払う」 が含まれてしまうので、
答えは
40－1＝39 (通り)
となります！

ちなみにもう1つ
正しい両替えパターンがあります。
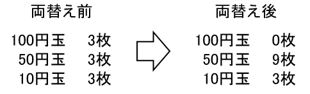
それは以下の 【例3】 のようにすることです。

【例3】

100円玉3枚をすべて50円玉に両替えしたんです！
これでも注意すべきポイントはクリアできていますからね！

この両替えをした後で同じように式を立てると…

（0＋1）×（9＋1）×（3＋1）＝40 （通り）
40－1＝39 （通り）

ほら、答えは同じになりました！！

答えは1つでも、
考え方は1つじゃない！

それもまた算数の魅力♪

実は
前回と今回の2回でご紹介した
“支払うことのできる金額”
ですが、
これは別のテーマにつなげるための前振りだったんです。

次回はそれについてお話できればと思います。

それではまた次回！