こんにちは。RS講師です。

今回はてこ難問シリーズ③
移動する支点です。

【問題】
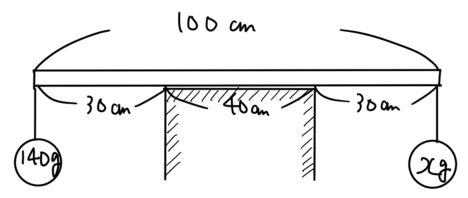
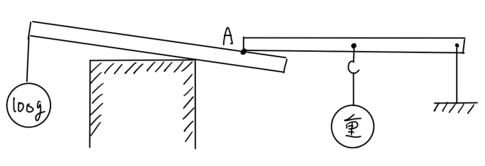
図のように、幅40㎝の台の上に、重さを考えなくてよい、長さ100㎝の棒が乗っています。
左端に140gの重りを下げています。
この棒が、台の上にとどまるとき、ｘのおもりの範囲を答えなさい。

さて、いきなり問題ですが、このような問題はどのように考えて行けばよいのでしょうか。
おもりが軽い場合と、重い場合にわけて考えて行きます。

＜おもりが軽い場合＞

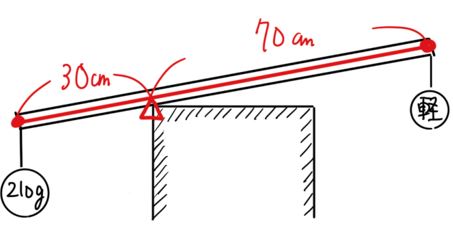
重りが軽いということはてこは左に傾きます。
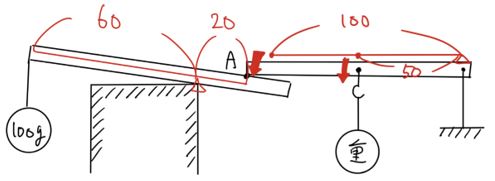
このとき、棒は図のように台の左端を支点にして傾くはずです。
棒が少しでも左に傾いてしまえば、そのまま左へ傾き続けて落ちてしまうので、おもりが最も軽いときは、台の左端を支点にしたときの釣り合いを考えればよいことになります。
したがって、210×30＝□×70　→　□＝90ｇ　となります。

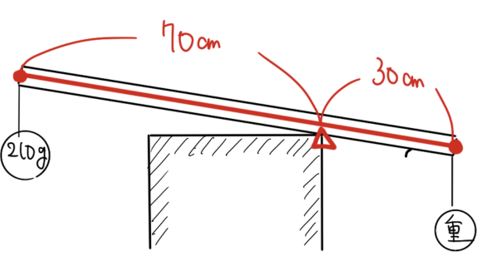
〈おもりが重い場合〉軽いときの逆を考えます。
おもりが重いのでてこは右へ傾きます。
このとき、支点は台の右側です。
210×70＝□×30　→　□＝490g
つまり、右側のおもりが490のときに、この棒は台の右端で釣り合いをとっているということになります。

さて、以上が基本的な考え方です。
このように、台の幅があると、重さが一定の幅で、棒がどちらにも傾かない状態が現れるのですが、おもりが軽いときと重たいときの間で、支点が徐々に移動するようになるわけです。

では、ちょっと応用問題を考えてみましょう。
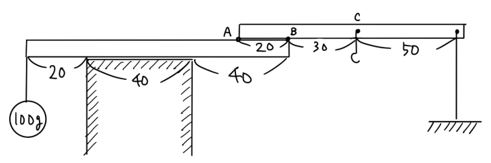
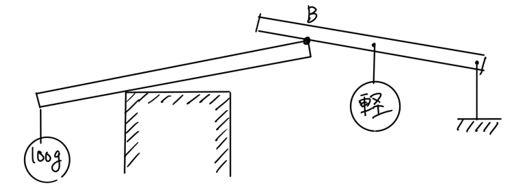
〈問題〉図のように2本の棒があり、一本は台の上に、もう一本は支柱に支えられていて、棒どうしもAB間で接していて支え合うようになっています。点Cにはおもりをぶら下げるフックがついています。この棒が釣り合うのは、Cにぶら下げるおもりが何g〜何gのときですか。ただしおもりの重さ以外は考えなくてもよい。

最も重いときと軽いときを考えて行くのは同様ですね。
では、まず重たいときから考えてみましょう。
点Cを重たくすると、右の棒は反時計回転の回転力が発生します。
その時、左の棒は点Aで押さえつけられるようになりますので、下の図ような釣り合い方をしています。

では順番に回転力を求めていきます。

左側のてこの釣り合いは、100×60＝□×20　□＝300g
従って点Aは300gで押されていることになります。

次に右のてこの釣り合いを考えます。
A点は300gで時計回りの回転力を左のてこから受けます。
これに対抗している回転力は、Cにぶら下げたおもりから生じていることになります。
このつりあいは、
300×100＝□×50　という式で表されるので、□＝600gです。

では、次は軽い場合です。
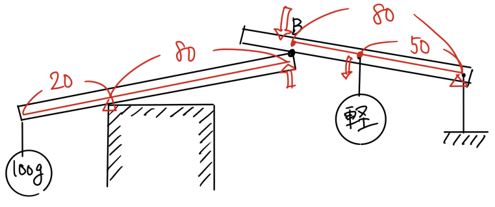
点Cのおもりが軽くなると、反時計回りに押さえつける力が減少するので、左側のてこの回す力に負けて図のように跳ね上がってしまうと考えられますね。
このとき、点Bで押し上げられることになるでしょう。

このてこの釣り合いは、下の図のようになっています。
まず、左のてこから・・・
100×20＝□×80　□＝25g

点Bは25gで押されることがわかります。
従って、右側のてこは、
25×80＝□×50　□＝40g

以上より、答えは25g〜40g　となります。

上の問題は、話を単純にするために、棒の重さは無しで考えましたが、
棒の重さがあっても考え方は殆ど変わりません。重心にかかる棒の重さが、上記の計算の左辺か右辺のどちらかに回転力として加算されるだけです。

さて、次回もてこのお話。
「重心の合成」というテーマを扱う予定です。
お楽しみに〜(^_^)/~