みなさん、こんにちは。受験ドクター算数科のA.K講師です。

 

前回に引き続き平面図形の重要な考え方について、今春の入試問題を例として取り上げます。

今日のテーマは、

 

共通部分

 

です！ではまず、練習から…。

 

【問題】

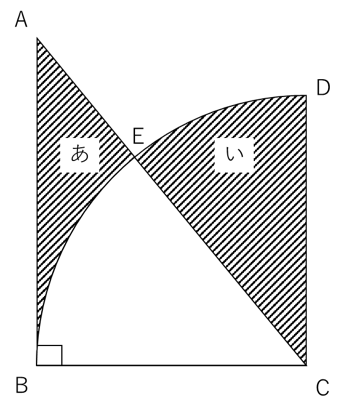
下の図のように、半径が6㎝でCを中心とした四分円BCDと、直角三角形ABCがぴったり重なっています。斜線部分「あ」と「い」の面積がそれぞれ同じであるとき、ABの長さを求めなさい。円周率は3.14とします。

 

 

さて、「あ」の部分も「い」の部分も、変な形をしているので直接面積を求めることは出来なさそうです。（「い」の部分は半径をCDとするおうぎ形ではありますが、中心角が分からないので求積は難しそうです）

ここで着目するべきポイントは、図の中で実際に面積を求められるのがどこであるか？ということです！それは、四分円であるBCDです。

「い」は分からないけど、おうぎ形BCEを足せば四分円になって面積が求められる…

→「あ」が「い」と同じ面積なら、「あ」に先ほどと同じおうぎ形BCEを足して出来る直角三角形ABCは四分円と同じ面積なのでは！？

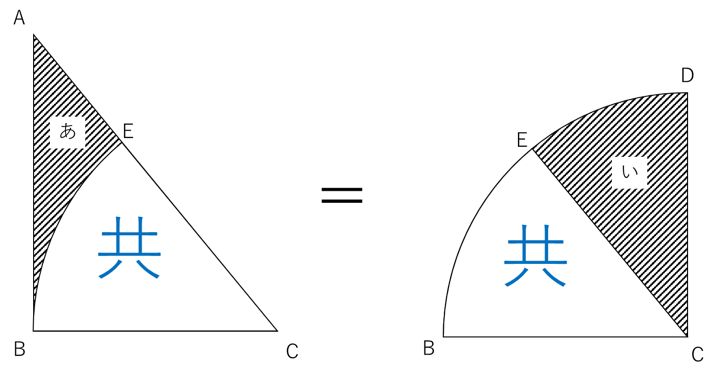
ということです。これを図にすると以下のようになります。

 

 

上図でも示されていますが、「あ」と「い」に加えた部分である白い部分おうぎ形BCEを共通部分と呼ぶことにします。

さて、このまま四分円BCDの面積について円周率を使って求め、逆算してABの長さを出すことも出来ますが…一つここは計算の工夫をしてみましょう！それは、各々の図形の面積の求め方について立式をしてみるということです。

直角三角形ABCについては、AB×6÷2

四分円BCDについては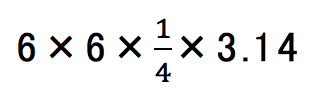
両者が等しいので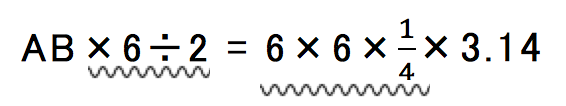

波線を引いた箇所を簡単にすると、AB×3=9×3.14

二重線を引いた箇所についてそれぞれを3で割ると、AB=3×3.14=9.42㎝と、簡単に答えが求まります！

このように、上手く工夫をすることで計算ミスをせずに答えを求めることが出来るんです。

 

～今回のまとめ～

・図形の問題において、面積がパッと求まらなさそうな部分が2か所以上あり、かつ各々が等しい場合であれば“共通部分”を探して面積が分かる図形に出来ないかを考えてみる。

・各々の図形を求める式を立て、計算の工夫が出来るところをして答えを求める。

 

いかがでしたでしょうか？今回の共通部分という考え方、平面図形の単元の中のみならず、ありとあらゆる場面で使えますからしっかりと理解しておきましょうね。

今回はここまでといたします。次回は本番として今春の入試問題を紹介し、さらに詳しくお話ししたいと思います！出題するのは…1月入試の中で、千葉県は京成大久保駅近くにあるあの中学校です！！

 

ではまた、お会いしましょう♪