皆さま、こんにちは!
「そもそも偏差値ってなに?」ということを考えていくシリーズ、今回はその第5回です。
偏差値の創案者として知られる桑田昭三先生のご意見も引用しつつ、偏差値の扱い方を考えています。
第3回で、現代の中学受験でどう偏差値をとらえるべきかについて、以下の4点をポイントに挙げました。
①そもそも偏差値はぶれるもので、最大で偏差値6くらいの上下は自然に起こる
②偏差値同士の比較には注意が必要で、特に同内容の試験でなければ推移を追うことにあまり意味はない
③偏差値を利用して受験の合否を判断する場合、向いている試験と向いていない試験が存在する
④偏差値はひとつの指標であって、試験内容、順位、平均点など、他の要素と総合的に考える必要がある
この4点は創案者の桑田先生のお考えをもとに、私の知識や経験も加えて解釈したものです。
そこまで詳しいことは必要ないという方は、最低限、この4点を覚えておいて頂ければ十分です。
今回は、この4つのポイントのうち、②についてより詳しく説明していきます。
なお、今回のブログでも以下の2つの参考資料を用いています。
1つは、1976年に徳間書店から発刊された『創案者が初公開する進学必勝法 偏差値の秘密』です。
以下、『偏差値の秘密』とします。
資料の2つ目は、インターネット上で公開されているインタビュー記事です。
2010年にJALTというNPO団体が桑田先生に行ったインタビューをもとにして書かれています。
現在も公開されていますので、興味のある方は以下のURLをご参照ください。
https://teval.jalt.org/test/PDF/Kuwata-j.pdf
以下、『桑田昭三氏へのインタービュー』とします。
偏差値のアップダウンを気にするのではなく
毎月のようにテストの偏差値が出る場合は、どうしてもそのアップダウンが気になります。
四谷大塚の週テストは、名前の通り毎週あるので、偏差値のアップダウンを1週間ごとに感じることになります。
しかし、偏差値のアップダウンに過敏に反応するのは、意味がないどころか、悪影響の方が多いです。
前回ご説明したように、そもそも偏差値3くらいの上下は自然に起こります。
そして、それ以外にも偏差値のアップダウンに影響を与える要素はあるということです。
まず、テストの内容を考えずに、偏差値の推移を追ったり、比較をしたりすることには、あまり意味がないです。
推移を追うことに意味があるのは、受験者やテストの難易度・出題構成が一定であるテストだけです。
6年生になってからのサピックスオープンや、合不合判定テストなどの実力試験がこれにあたります。
他塾であっても、合格可能性が出る合否判定テストのようなものはすべて同じです。
こういった実力試験は、偏差値推移を追うことに一定の意味があります。
しかし、出題範囲が限定されたテストの偏差値は、推移を追うことにはあまり意味がありません。
サピックスのマンスリーテストや、四谷大塚の週テストなどの、出題範囲が限定された試験がこれにあたります。
こういったテストの偏差値は、あくまでその範囲での自分の出来・不出来を示すだけです。
今後の学習の参考にはなりますが、それ以上の意味はあまりありません。
話をわかりやすくするために、極端なケースで考えてみましょう。
たとえば、算数のテストで、ある月のテストの出題範囲が「平面図形」だったとします。
このときの偏差値が60だったとしましょう。
翌月にまたテストがあり、この月はテストの出題範囲が「場合の数」だったとします。
そして、今回のテストでは、偏差値が40と出たとします。
この場合、偏差値が60から40に下がったといえるでしょうか?
見た目の数字はもちろん下がっていますが、算数の実力そのものが下がったかどうかはわかりません。
ここから言えることは、「平面図形」はよくできるが、「場合の数」は苦手なのかもしれないな、ということだけです。
あえて極端なケースで例えましたが、全範囲の実力試験でない限り、おおむねこの傾向はあります。
特に4年生・5年生の間のテストは、ほとんどがこのような試験になります。
ある程度の広い範囲で出題がある、サピックスや四谷大塚の組み分けテストでも、同様の傾向はあります。
そうだとすると、これらのテストの偏差値の推移や、前後の試験の偏差値の比較にはあまり意味がありません。特に、4年生や5年生のうちは、偏差値のアップダウンには一喜一憂しすぎないように気を付けましょう。
推移を気にするとしても、範囲が広い組み分けテストのような試験の偏差値だけにした方が良いです。
範囲がある試験については、先ほども書いたように、定着度のチェックくらいに考えるべきです。
そして、大切なのはテストのあとで、偏差値が低く出たときの単元が要復習であるのは間違いありません。
偏差値を気にするよりも、できなかった範囲のテキストやプリントを引っ張り出して復習をする方が建設的です。
間違えた問題や偏差値が低く出たテストの問題こそ、学力向上のカギをにぎる宝物です。
そこを鍛えれば、確実に自分の実力アップができる問題だからです。
数字が低く出たときは、むしろやるべきことがはっきりした、とポジティブに考えた方が良いでしょう。
実力試験だとしても…
先ほど、「実力試験は、偏差値推移を追うことに一定の意味があります」と書きました。
しかし、実力試験の場合でも、単純に偏差値の推移を見て一喜一憂するのは気を付けた方が良いです。
前述のように、受験者やテストの難易度・出題構成が一定であるテストでないと、安易な比較はできません。
たとえば、受験者の層が変われば、当然偏差値は変わります。
一番わかりやすいケースは、各塾の試験による偏差値の違いです。
たとえば、サピックスの偏差値と、四谷大塚の偏差値は、おおむね5〜10くらいの差があります。
同じお子さんが試験を受けても、サピックスの方が偏差値が5〜10くらいは低く出ます。
これは受験者層の違いの影響であって、お子さんの実力が下がったわけではありません。
同じ塾の実力試験を受け続ける場合は、試験ごとにここまで極端に受験者層が変わるわけではありません。
しかし、外部生にオープンな模試の場合は、回によって受けているお子さんの数やレベルが微妙に変化します。
ですので、その回の受験者の数やレベルによって、多少の偏差値のアップダウンはあると思った方が良いです。
また、問題の出題構成や難易度も、偏差値には影響します。
そしてそれが、ある程度一定のものに保たれていないのであれば、偏差値を安易に比較することは危険です。
特に、受験者の得点分布が、正規分布曲線を描いていないなら、偏差値の精度は低くなります。
正規分布曲線というのは、得点分布をグラフにしたとき、下のような釣り鐘型の曲線になることです。
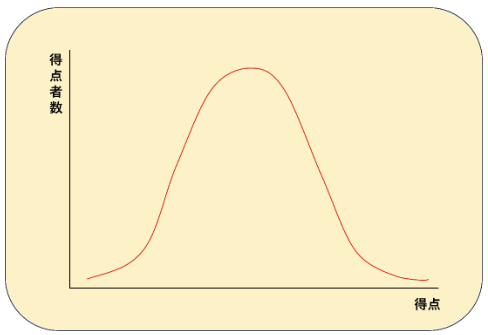
実際のテストの得点分布が、この正規分布曲線から外れれば外れるほど偏差値の精度は下がります。
なぜかというと、受験者の得点分布は正規分布するはず、という仮定のもとに偏差値を計算しているからです。
ですから、得点分布がどちらもある程度は正規分布に近い状態でないと、偏差値同士の比較も難しくなります。
実際に、創案者の桑田先生も著書の中で次のように書かれています。
偏差値の理論が適用できるということは、得点分布図を正規分布図とみなすことができること
が前提になっている。理論の上では確かにそうした曲線を描き、その限りにおいて偏差値は意味
持つ。しかし、じっさいには、正規分布を描かない場合もあるのである。
【中略】
これは試験の作り方にも関係してくることである。つまり、偏差値がそのままでは偏差値と
して使えなくなってしまうような試験問題自体に問題があるのである。私たちは試験問題を作
る場合、大体、平均点が50〜60点ぐらい、できなかった生徒で20点ぐらい、よくできた
生徒で95点ぐらいとれるもの、というのを一つの目安にしている。それが、100点がぞろ
ぞろ出たり、0点や5点がぞろぞろ出たりする出題をするようでは、教師としてのカナエの軽
重を問われる。それは、生徒の実態をまったく把握していない証拠だからである。つまり、試
験問題が生徒の学力水準とかけ離れていたか、よほど指導方法がまずくて生徒が教えられたこ
とを理解しえなかったかのどちらかなのである。
私自身は、今もそれは変わらないが、つねに得点が真ん中あたり、つまり50点前後に集中
する問題を作ることを心がけている。
偏差値を用いた指導をつづけるためには、生徒の実態を的確にとらえて、もっとも望ましい
得点分布になるような出題をするよう、先生方に気をつけてもらう以外に策はないと思った。
【中略】
しかし、こうして自分たちで注意を払いながら作った問題でも、正規分布しない科目が、
どうしても出てきた。こうなると、偏差値を理論通りに使うことはできない。
(『偏差値の秘密』140〜143ページ)
数学的には、正規分布しない場合は、正規変換という処理をすれば、ある程度は解決します。
しかし、ここでは専門的な話は避け、偏差値を出すことに向いているテストがある、と理解しておけば十分です。
偏差値の精度が高いテストは、次の3点を満たしている必要があります。
①真ん中の得点付近に、多くの受験者が集中している
②得点が真ん中からずれればずれるほど、受験者の数が減少していく
③得点が高い方にも低い方にも、おおむね均等に分布している
逆に言うと、得点者の分布が下のグラフのような形になる場合は、その偏差値にはあまり意味がないです。
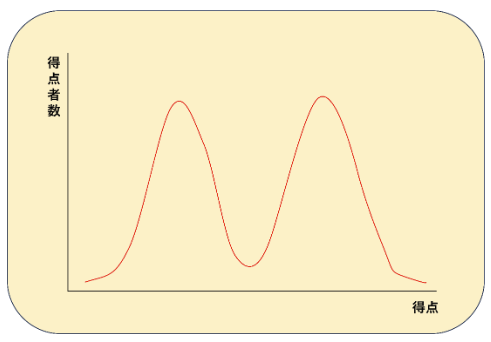
ここまで二極化した得点分布はそうそうありませんが、もしこうなった場合、偏差値はあまり意味をなしません。
それよりも、自分が高い方と低い方のどちらの山に入っているか、の方が重要でしょう。
低い山の方に入っている場合は、少し危機感を持って勉強しようと捉えれば十分です。
もちろん、この前後に受けているテストの偏差値との比較も意味がないです。
比較するテストが、正規分布に近い得点分布のテストだった場合はなおさらです。
ただし、得点分布が正規分布になるテストをつねに作り続けられるかというと、これはかなり難しいです。
指導要領の範囲に出題が限定されており、出題構成があまり変化しない公立高校の模試なら可能です。
しかも、模試の受験者は、ほぼすべての受験生、つまり実際の公立高校の全受験者とほぼ一致します。
以前も書いたように、だから、公立高校の入試における模試の偏差値や合否判定の精度は非常に高いのです。
しかし、中学入試のテストの場合は、その性質上、なかなかそういった模試を行うことが難しいです。
だとすれば、その偏差値の推移を追うことや、偏差値同士の比較をすることには注意をする必要があります。
偏差値が、おおまかな傾向を教えてくれる非常に参考になる数値であるのは間違いないです。
しかし、中学入試においては、そもそも偏差値は測定誤差が大きい不安定なものと思っておきましょう。
大切なことは、偏差値が下がったときに、きちんとその原因を分析することです。
実力が下がったこと以外にも、単なるブレや誤差、受験者の変化、問題の変化など、原因は複数あり得ます。
得点、順位、出題された問題の内容やレベル、得点分布などを、多角的にチェックすることが重要になります。
そういった分析が難しいという場合は、正しい分析ができるプロの先生に相談しましょう。
とにかく、数字が上がった・下がったということだけに一喜一憂することはできるだけ避けましょう。
次回はポイント③について、詳しく解説します。
では、また次回お会いしましょう!




