皆さま、こんにちは！

さて、前回は「面積比」の前置きとして、そもそもの面積の求め方から解説しました。
今回からは、本格的に「面積比」についての解説をスタートします。
前回もお伝えしたように、面積の基本は「たて×よこ」（あるいは「底辺×高さ」）です。
これは「面積比」になっても変わりません。
まずはこのことから確認してみましょう。
基本に忠実に考えることを大切にしてくださいね。

例えば、以下のような問題を考えてみましょう。

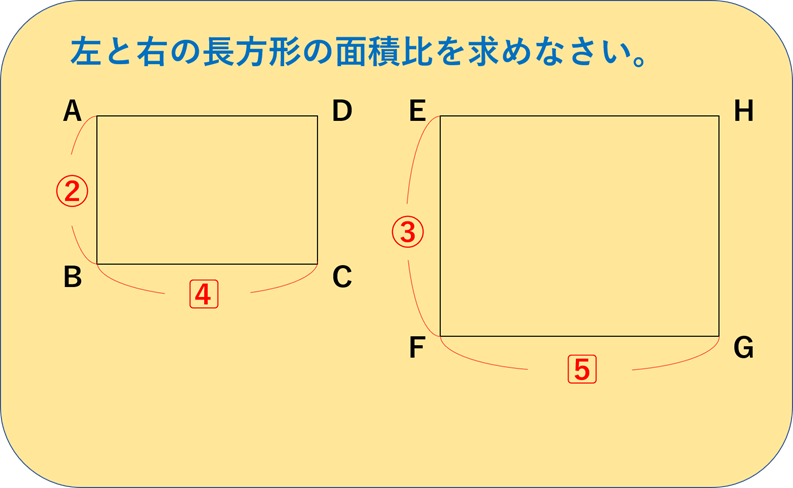
２つの長方形のたての長さの比は２：３です。
よこの長さの比は４：５です。
面積は「たて×よこ」で求められるので、「面積比」も「たての比×よこの比」でOKです。
ですから、左の長方形は２×４＝８、右の長方形は３×５＝１５と考えます。
よって、ふたつの「面積比」は８：１５です。
これだけです。
簡単ですね！
いまいちピンとこない場合は、それぞれの比に単位をつけて考えてしまいましょう。
例えば、すべての長さに㎝をつけてみたらどうでしょう？

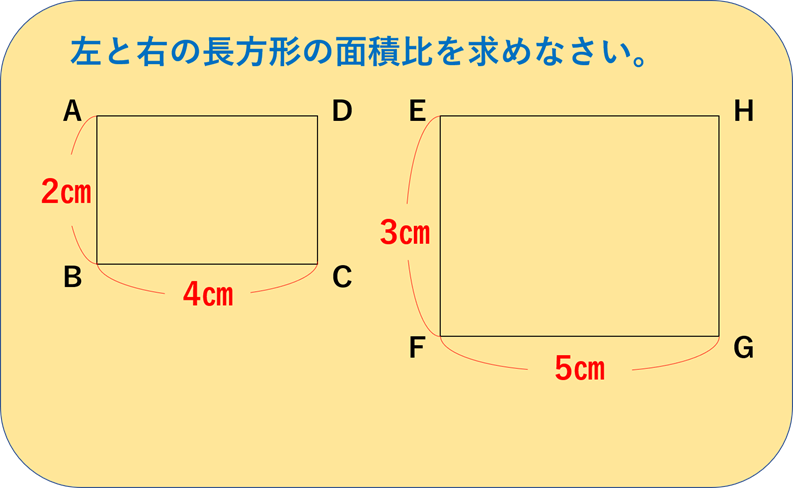
すると、左の長方形は８㎠、右の長方形は１５㎠です。
具体的な面積にしてみても、やはり「面積比」は８：１５ですね？
自然に当たり前に考えれば大丈夫です。

さて、もちろん実際にはこんな簡単な問題は出題されません。
さらに複雑な「面積比」を考える場合には、もう少し深く考えていく必要があります。
より複雑な「面積比」を考える際の、最初の１歩は「双子山」です。
「双子山」は非常に重要で、これを知っているだけでも
ほとんどの「面積比」の問題は解けます。

まずはここから考えてみましょう。
「双子山」とは、以下の図のような形を指します。

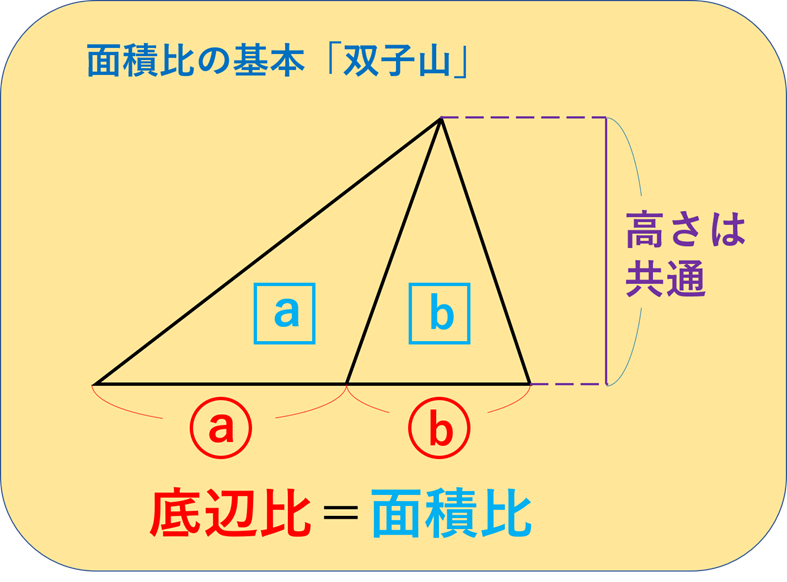
左と右の三角形の面積比は、ふたつの三角形の底辺比と同じです。
必ず底辺比＝面積比となります。
なぜでしょうか？
はい、高さが一緒だからですね。
三角形の面積は「底辺×高さ」で求められます。
ふたつの三角形の高さが一緒なら、面積の違いは底辺だけで決まります。
ですから、底辺比＝面積比でいいのです。

「あれ、÷２はいいの？」と思われた方もいらっしゃるかもしれませんが、これでいいのです。
実際に三角形の面積を求めるなら、必ず「底辺×高さ÷２」としなくてはいけません。
しかし、「面積比」がわかればいいのなら、「÷２」は必要ないのです。
どちらも「÷２」をするのなら、それはしてもしなくても同じことです。
「比」の問題のお約束として、「答えはもっとも簡単な整数比にする」というものがあります。
比を簡単にする際、左右どちらの数にも同じ数をかけたり割ったりするのなら、何をしてもOKです。
ですから、どちらも「÷２」をしているなら、それはしてもしなくても同じことなのです。

もしかすると、「比」が苦手な人というのは、この辺りのことがピンと来ないのかもしれませんね。
「比」は具体的な量ではなく、あくまで２つの数を比べた割合なので、こういったことが成り立つのです。
前回、面積はとにかく「たて×よこ」ですよ、と強調したのも、これが理由です。
「面積比」を考える場合は、どちらにも共通することがあるなら、そこは省略してOKです。
三角形同士を比べるなら、「÷２」は共通しているので考えなくても良いのです。
そして、今回の「双子山」は「高さ」も共通です。
すると、「底辺×高さ÷２」のうち、「×高さ÷２」は省略して良い、ということになります。
そう考えると、残っているのは「底辺」だけですね。
したがって、「底辺比＝面積比」ということが成り立つのです。

基本中の基本のことなので、ここまで丁寧に説明しなくてもわかっているお子様が大部分だとは思います。
しかし、ちょっとでも理解があやしいと感じたら、「どうしてそうなるの？」と必ず聞いてあげてください。
そのときに、完璧ではなくても、自分なりに理屈を説明できているならOKです。
逆に、「なんとなく」や「そう教わった」など、理屈がないなと感じたら、必ずそこから復習してください。
ちょっとしたことでも、ちょこちょこと確認を入れていくことで、理解は必ず深まります。
そういったことの積み重ねでしか、深い応用力も養われません。
いつでも「なぜ？」という問いを頭に持っておくようにしましょう。

最後に、１題だけ宿題を出しておきます。
この問題が正しく解けるかどうかを、ぜひチェックしてみてください。
解答は以下の問題のさらに下につけておきます。
解説は次回の冒頭で行います。
ぜひやってみてください。
それでは、また次回お会いしましょう。

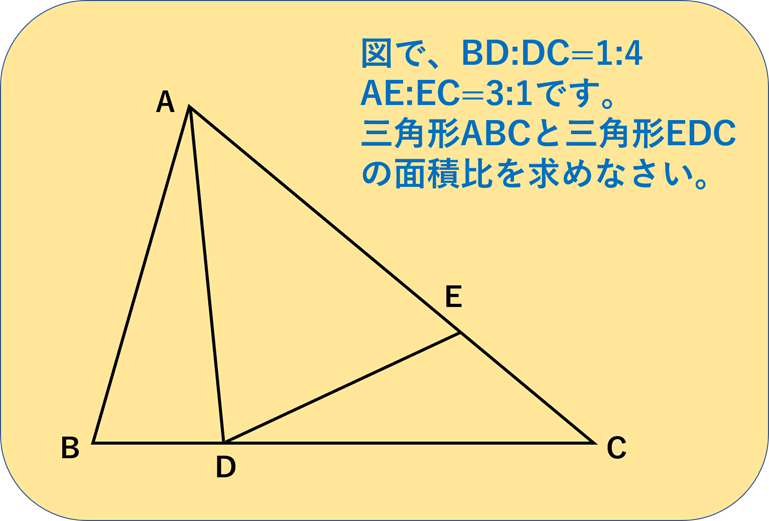
答え   ５：１