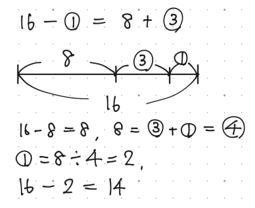こんにちは。
受験ドクター算数科のRS講師です。

冬期講習も終わり，入試まで後少しとなってきましたね。
今日は直前期にワンポイントで理解を深められるようなお話をしたいと思います。
導入期の5年生にも有効ですので，是非活用してみてくださいね。

ではいきましょう。
流水算についてです。

まずはコレ。

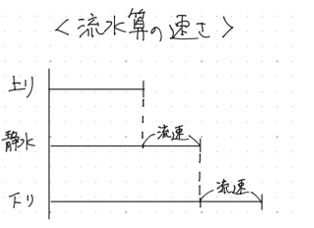
流水算の速さを線分図で表したものです。
見たことはありますよね？

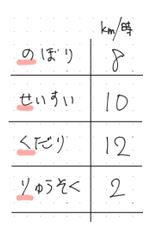
静水時（流れがないところ）での速さが時速10kmだとします。
川が時速2㎞で流れているとすれば，上りは流れに逆らって進むから遅くなるので，10ー2＝8㎞/時，下りは流れにそって進むので速くなります。10＋2＝12㎞/時ですね。

いま，何種類の速さが出てきましたか？
「上り」，「静水」，「下り」とさらに「流速」という速さも出てきました。全部で4つあります。
流水算は，この4つの速さの関係が連動して変化する文章題と言えます。

この4つの速さですが，
このうち2つが分かると，残り2つは自動的に求められるという法則があります。
上記の例のように静水時と流速が分かっていたので，上りと下りが求められました。
とくに，静水は上りと下りに挟まれたちょうど真ん中の値なので，
（上り＋下り）÷2＝静水（平均の考え方）となります。
また，上りと下りの差は，流速2つ分隔てているのもポイントですね。

まあ，このまま公式のように覚えてしまうのも手ではありますが，理解を伴わない公式暗記は算数ではやってはいけない学習法です。
流水算の導入では，上に書いた速さの線分図と共に，数量関係をしっかり意識させながら学習を進めることが特に重要です。

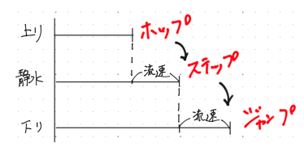
さて，慣れてくると，この線分図，毎回きちんと書くほどの複雑な情報は含まれていません。
ようするにホップ・ステップ・ジャンプの3段階になっていて，それらが等間隔というだけの話です。

なので，これは線分図を逐一書くのはサッサと卒業してしまって，下の図のような表にしてしまいましょう。

これを速さの名前の1文字をとって，「のせくり表」と言います。
この表は線分図を書くよりも，簡単に書け，複数書く場合でも時間がかかりません。
また，流速が変化する問題，こぐ速さが変化する問題，どんな場合も上手に整理できます。

一つ例を取り上げてみます。

 

【例題1】
川の上流のA地点と，その120㎞下流のＢ地点があります。船ＰがＡからＢへこぎ下るのに10時間かかり，上るのに8時間かかった。船ＱはＡ地点からＢ地点へ下るのに，15時間かかった。船ＱはＢ地点からＡ地点へ上るのに何時間かかるか。

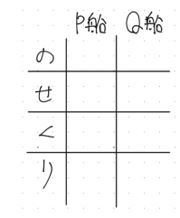
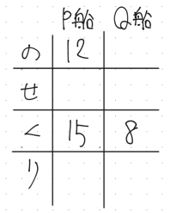
①　まず，のせくり表をＰ船用とＱ船用に二つ用意します。

②　問題文から求めた速さを書き込んで行きます。このとき，表に書くのはあくまでも「速さ」であることに注意しましょう。のせくり表は4つの速さ表す線分図を表にしたものであるということを念押ししてください。

120÷8＝15ｋｍ/時（Ｐ船くだり）
120÷10＝12ｋｍ/時（Ｐ船のぼり）
120÷15＝8ｋｍ/時（Ｑ船くだり）

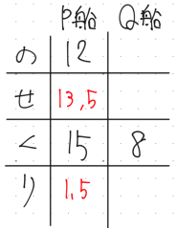
③　のせくり表は4つのうち，2つ決まると，残りはすべて決まります。Ｐ船ののせくりを埋めてしまいます。

（12＋15）÷2＝13.5ｋｍ/時
（15ー12）÷2＝1.5ｋｍ/時

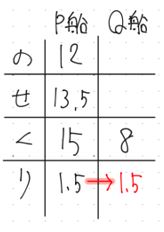
④　Ｑ船ののせくりは1つしか分かっていないので，残りを求める事はこのままではできません。
Ｐ船ののせくりから使える情報がないかを考えます。
ここでは，同じ川を上り，下りしているので，流速は同じです。

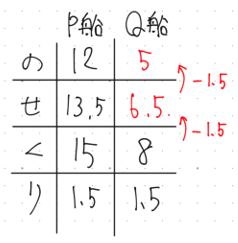
⑤　Ｑ船ののせくりが2つ埋まりましたので，残りをすべて埋めます。Ｑ船が上りに何時間かかるかを求めるので，120÷5＝24時間が答えとなります。

さあ，こんな要領でやっていけばいいのですが，ちょっと難しいものもやってみましょう。
 

【例題2】
ある船が上流のＡ地点と，48㎞下流のＢ地点を往復しました。ＡからＢに下るときは3時間かかりました。帰る時は川の流れが3倍の速さになっていたため，Ａ地点に帰るのに6時間かかりました。この船の静水時の速さは時速何㎞ですか。

船が一つなので，のせくり表は1つと思うかも知れませんが，
ここでは，流速が変わったとありますので，流速の変化の前後でそれぞれのせくり表をつくるのがポイントです。のせくり表は，4つの速さの連動がポイントですので，何かが変化する度に別々のせくり表を作ります。

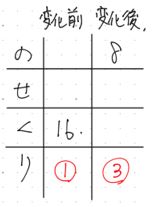
①　のせくり表を2つ用意して，求める事の出来る部分を求めます。
48÷3＝16km/時　下るとき（変化前）
48÷6＝8㎞時　上るとき（変化後）

②　どちらののせくり表も1つしか数字が埋まっていないので，その他の枠を埋める事ができないですね。
ですが，流速については，もともとの流速が3倍になったことがわかっています。比を使って，元の流速を①，変化後の流速を③としておきます。

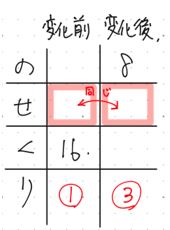
③　二つののせくり表に共通のものは何でしょうか。
ここでは，静水時の速さです。
流速が変化するまえも，後も静水時の速さは変わっていません。
16ー①と8＋③は同じ値です。

16ー①＝8＋③
④＝8，①＝2
この式がすっと解けない場合は，下図のような
線分図を書いて理解するように努めましょう。

静水時の速度は，16ー2＝14㎞/時です。

はい。どうでしょうか。
線分図を書いてごちゃごちゃ悩むよりも完結に解けるのではないかと思います。
流水算の難問も含めてこのように整理しておけば，上りと下りで取り違えてしまったとかというミスもかなり防げるはずです。

流水算が苦手という人も，復習する5年生も，ぜひともこの方法を身につけてみてください。

ということで，本日はここまで。
ではまた〜(´∀｀*)ﾉ