みなさん、こんにちは。受験ドクター算数科のA.K講師です。

新年、あけましておめでとうございます！今年もどうぞ宜しくお願いいたします。６年生の皆さん、本番まで１か月を切りましたが、一緒に走り抜けましょう。

今日は、場合の数について、入試直前に覚えておいてほしい知識についてお話ししましょう。
それは、「直前の結果を利用する」というものです。

問題１
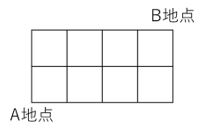
下のような道路があります。A地点からB地点まで、最短の経路で行く方法は何通りありますか。

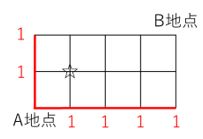
道順の考え方でよくある問題です。まず、Aから縦と横にある道上の分岐点は以下のようにすべて1通りになります。

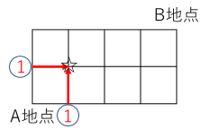
続いて、上図の☆の地点については、以下のように○で囲んだ地点を必ず通ることになるので、1+1=2通りとなります。これが直前の結果を利用するということです！

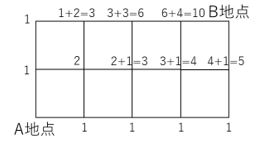
同じようにして他の地点も全て埋めてみると…

よって、B地点までの行き方は10+5=15通りとなります。

ただ、これはほんの序の口…。
では次の問題にLet’s try！

問題２
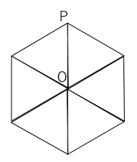
下のような正六角形の形をした道路があります。1秒間で、1つの頂点からとなりの頂点に移動で
きるものとします。点Oを出発したとき、3秒後に点Pに移動する方法は何通りありますか。

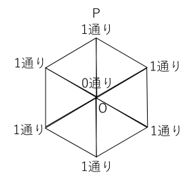
こういった問題を考えるときには、まずは1秒後に各頂点にいく方法が何通りであるのかを図にしてみます。

正六角形の各頂点とも、中心である点Oから1秒かけて進むのでどれも1通りです。（中心である点Oは、出発点なので1秒後に行くことは出来ないので0通り）
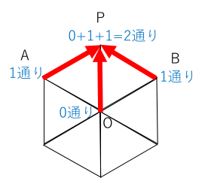
次に2秒後の状態ですが、下図のように点Pにくるには1秒後に点O、点A、点Bのいずれかにいる必要があります。したがって、1秒後の図から0+1+1=2通りとなります。

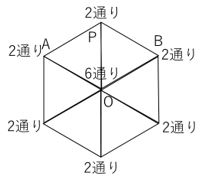
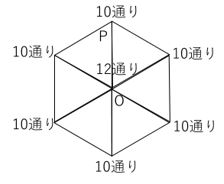
点Oについては、1秒後に正六角形の頂点のいずれかにいればよいので、1+1+1+1+1+1=6通り。他の点も同じように考えると…

先ほどの考え方を用いると、3秒後に点Pにいるには2秒後の状態で点O、点A、点Bのいずれかにいれば良いので、6+2+2=10通りとなります！（点Oは2+2+2+2+2+2=12通り）

いかがでしたでしょうか？こういった知識、入試に必ず役に立つと思います。この辺で今日の総括に移らせていただきます。

～本日のまとめ～
・場合の数における道順の問題は、前の結果を利用して答えを求め、またその結果を次の答えに活かしていく。

今回はここまでといたしましょう。次回は、2020年の入試もひと段落したころの記事となりそうですので、入試問題をトピックとしてお伝えできれば思っております。

ではまた、お会いしましょう♪