こんにちは。受験Dr.の坂井です。
前回のブログで、復習の重要性について述べましたが、今回はワンランク上の算数をめざすためには何を意識して復習を行うと良いかについてのコツをお伝えしようと思います。

ところでワンランク上の算数とはいったい何？というところからお伝えします。ワンランク上というのは典型題の標準レベル問題を戦い切ることができる状態にするということを意味しています。テストでいうと中盤くらいに登場してくる大問が解けるようになる、または、全部正解できなくとも問題の題意が読み取れ(1)と(2)くらいまでなら解けるようになるということです。

「復習」の意識を変えてみよう

授業内で行われたテストの間違えた問題を復習することはもちろんですが、授業で習った新しい単元の考え方を復習することが何よりも重要です。例えばテキストの例題を用いて新しい単元内容の考え方を学習したのであれば、家庭学習でいきなり課題の問題練習をするのではなく、授業で解説された例題を再度確認することが効果的です。なぜなら、どの部分がポイントになるかを確認しなければならないからです。ポイントを押さえたうえで問題練習をするからこそ、自力で解ききるための力が養成されます。ポイントを押さえず課題の問題が解けたとしても、それは習った直後であるため解法を覚えているから解けるのです。解けるということはよいことなのですが、それだと典型題であろうとひとひねりされた出題をされたら太刀打ちできないことにもなります。習ったことをすぐに復習することの重要性は前回のブログでも述べましたが、もう少し堀下げていうと、「習った解き方を忘れないうちにすぐ復習」ではなく、「ポイントを忘れないうちに復習」することが大切です。
すべての問題についてどこにポイントがあるのかを気にして復習することを意識してください。

どのようにポイントを意識するのか

次の問題を例に、どこにポイントがあるのかを考えていきましょう。

(問題1)は数値が書いてありません。ポイントだけ考えてみてください。

ポイント
①円すいの側面積：　母線×半径×3.14
②相似比、面積比の利用（面積比を利用しなければ、全体の円すいの側面積から上側の側面積をひく）

以上2点が瞬時に頭をよぎることがテストでは必要になります。
円すい関連ということになると、
この問題を解くためには直接関係はありませんが、
円すいを見た瞬間に、展開図にしたときの側面部分の中心角の大きさが

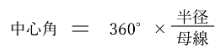
であることも、同時に頭をよぎることでしょう。

以上のことが瞬時に出てこないとテストでは、
1. 心にゆとりがもてない、あわてるなどのことも相まって
2. いつも正解できない
または
正解できるときもあるが、できないときもある。
という状態になります。

円すいの側面積の求め方を忘れたという受験生の多くは、復習の際に求め方の式に当てはめて課題をこなしてしまったことが原因なのです。

こんどは速さの問題で考えてみましょう。

ポイント
2人が反対方向に進む往復の問題です。
ポイントは次の通りです。
①2回目に出会うまでに、2人の動いた距離は家から駅までの距離の3倍
②したがって、2人がはじめて出会うまでの時間は2回目に出会うまで時間の

⇒xの値は、10(分)
往復の問題を見た瞬時に上の①②のことが頭をよぎることがなければ、解答の糸口が見つからず「解けない」ということになります。
すなわち、復習の際になぜ３倍，倍になるのかということを理解すること、ここがポイントになるということを意識しておかなければ、テストなどのいざというときに解答までたどり着けないことになるのです。

ちなみに、(問題2)の解答は　【答え】　(1)10　(2)1400ｍ　です。
ぜひ解いてみてください。

立体図形の問題でも見てみましょう。

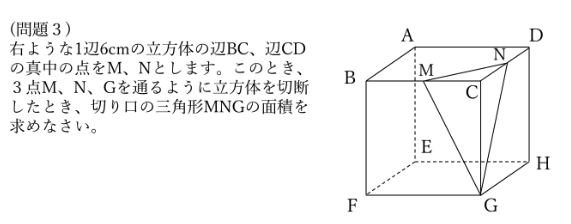
ポイント
ポイントは次の通りです。
①切断してできた三角すいが
CM：CN：CG ＝ 1：1：２　の特別な三角すいであること
②展開図が1辺6cmの正方形になること
そして、三角すいの展開図を利用しないと解けないこと

②に意識がなく、辺MNの長さや三角形MNGの高さを求めて面積を求めようとする受験生が多いのも事実です。
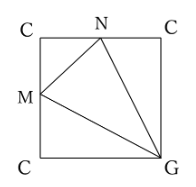
復習の際は、実際に展開図を自分の手で書き、正方形のどの辺が三角すいの高さ(CG)になるのかをしっかり認識することをおこなってください。

展開図を書くと右図のようになりますが、切り口である
三角形MNGの面積は、正方形の面積から周りの3つの
三角形の面積を引けば求めることができます。
正方形全体のになることを利用してもよいでしょう。
【答え】13.5㎠

まとめ

みなさんが解く問題それぞれにポイントなるものは存在します。ポイントが意識されない状態で課題を解いて問題演習を重ねても、テストなどの場面で解けなければ意味がありません。新しい単元の内容を習ったら、自らどこにポイントがあるのかを意識しながら復習を行ってください。同じような問題でも解ける時もあれば解けないときもあるというような場合は、ポイントが明確になっていないことが原因である可能性が大きいと思われます。そのような受験生は、どこにポイントがあるのかをいつも気にしながら復習することを実践してみてはいかがでしょう。そうすることによって得点力が上がっていくはずです。ぜひ、みなさんでワンランク上の算数をめざしていきましょう。

それでは、またお会いしましょう。