みなさん、こんにちは。

受験ドクターの坂井です。

9月以降、多くの受験生が過去問を解き始めていると思いますが、忘れたころに出題されている問題の1つにN進法があげられます。どうやって解くんだっけ？という受験生、多いんじゃないでしょうか。

次の問題を使ってN進法を確認していきましょう。
(1)と(2)は確実におさえておかないといけない問題です。(3)は少し面倒くさいですが、3の倍数の性質の確認、集計の練習になるので頑張ってみてください。
では問題。

(1)　これらは3進法で表された数字です。
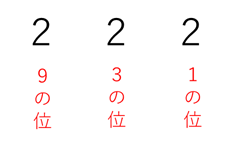
３けたの数字で最大の数字は２２２です。　　　　　　　　
　　「9の位」に２，「3の位」に２，「１の位」に２
　　という数字ですので、
　　９×２＋３×２＋１×２＝２６　となり、
　　１から数えて26番目の数になります。
　　１けたと2けたの数字は8個あるので、　２６－８＝18個　　　　　18個

　　
　　別解
　　3けたの数字では、「９の位」は１か２の2通り，「３の位」は０か１か２の3通り，
　　「１の位」は０か１か２の3通りであるので、　2×3×3＝18（個）と求めることもできます。

(2)　3進法で表す数の100番目の数です。
　　下の計算より、　　10201
　　　　　　　　　　　　　　　　　　　　　　　　　

(3)　これは少し面倒な作業が必要になりますが、差がつく問題です。
　 入試本番に向けて練習を積んでぜひ慣れてほしい問題です。

　　３の倍数は、各位の数の和が3の倍数であることを利用して考えていきましょう。

【1けた】　１けたの3の倍数はありません。

【2けた】　１２，２１の2個です。

【3けた】　3けたの数では3つ数が
　　　　（０，１，２）　（１，１，１）　（２，２，２）の3種類になります。
　　　　
　　　　（０，１，２）⇒　「９の位」は１か２のどちらか。２×２×１＝４通り
　　　　（１，１，１）⇒　　1通り
　　　　（２，２，２）⇒　　1通り
　　　　　よって　４＋1＋１＝６個

【4けた】　4けたの数での４つの数の組み合わせは、
　　　　　（０，０，１，２）　（０，１，１，１）　（０，２，２，２）　　（１，１，２，２）の4種類になります。それぞれについて調べていきます。

　　　　　（０，０，１，２）⇒　「27の位」は１か２。
1の場合、１００２,１０２０,１２００　　　　　　
2の場合、２００１,２０１０,２１００

よって　3×2＝6通り。　　

（０，１，１，１）⇒　「27の位」は１だけ。０が「９の位」「３の位」「1の位」のどこにくるかを考えると
１１１０，１１０１，１０１１の3通り。

（０，２，２，２）⇒　（０，１，１，１）のときと同様に3通り。

（１，１，２，２）⇒　１の場所を4か所から2か所選ぶ方法は
　　　　　　　　　　　４×３÷（２×１）＝6通り。
　　　　　　　　　　　　　　　　よって6＋3＋3＋6＝18個

【5けた】　100番目の数，10201までの5けたの数を並べてみると，
　　　　　　
　　　　　　10000，10001，10002，10010，10011，10012，10020，10021，10022
　　　　　　10100，10101，10102，10110，10111，10112，10120，10121，10122
　　　　　　10200，10201

　　　　　　青字の7つの数字が3の倍数になります。　　7個

　以上より、　2＋6＋18＋7＝33個　　　　　　　　　　33個

　　どうでしたか？
（３）は、調べて集計していかなくてはならないので大変だったと思います。
　その中でも５けたの３の倍数は、3の倍数の性質を利用して、各位の数の和が3の場合と、6の場合に着目して見つけていく方法もありますが、全部書いても20個くらいなので、このくらいの量だった書いて調べていってもよいかなと思います。

今回のお話はここまで。
それではみなさん、またお会いしましょう。