（発展的な）時計算④　～長針と短針が90°になるのは何回ある？～

みなさん、こんにちは。
受験Dｒ．の坂井智則です。

今回は時計算のおはなし第4弾です。
一定の時間の範囲で長針と短針のなす角が90°になるのは何回あるのかといったお話です。

長針と短針のなす角が90°になる回数を求める問題は、一見簡単そうに見えますが実は苦手にしている受験生は多くいるのではないでしょうか。

例えば、朝の6時から夕方の6時までの間に、長針と短針のなす角が90°になる回数を考えてみましょう。

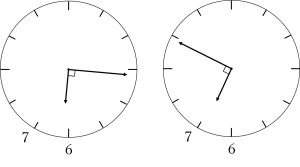
下図のように6時と7時の間に長針と短針のなす角が90°になる回数は2回あります。

ちょっと想像してみると7時と8時の間も長針と短針のなす角が90°になる回数は2回あります。
そうなんです。60分で2回あることがわかります。
ということは、6時から8時の2時間のあいだに90°になる時間が4回あるということになります。

さらに続けてみると、8時と9時の間にも2回あります。そして9時と10時の間にも2回あります。
では今回も8時から10時までの2時間のあいだに長針と短針のなす角が90°になる時間は4回あらわれる・・・・？？？　いや、4回ではなんですね。　実は3回しかありません。では、なんで4回ではないのしょうか。

その理由を示すには「9時」という時刻がポイントとなります。
9時ピッタリという時間は長針と短針の角が90°になっているのです。(当たり前ですが…)
この「9時」が8時から9時の間と9時から10時の間で重複してカウントされているのです。
ですから8時～10時の2時間のあいだに長針と短針のなす角が90°になるのは3回なのです。

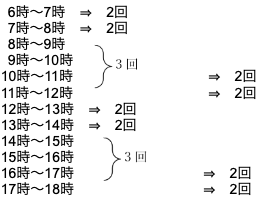
「9時」と同様に「3時」にも注意して、朝6時から夕方6時までの長針と短針のなす角が90°になる回数をすべて書き出してみることにします。

合計22回　ということになります。
書き出して調べてみてもあまり手間はかかりません。
みなさん、是非一度手を動かして書き出してみてください。

では、この22回を計算で出すにはどうしたらよいのでしょうか。
ここからは計算を用いて算出する考え方について見ていきます。

【計算方法】
朝6時から初めて長針と短針のなす角が90°になる時刻を求めてみましょう。
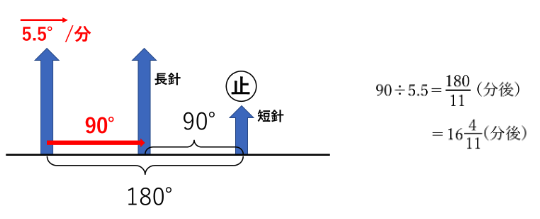
1分間に長針と短針はそれぞれ６°，0.5°ずつ動きます。ですから、長針と短針の距離は1分間に5.5°ずつ近づいたり離れたりします。6時の時点で短針と長針は180°離れているので、その距離をあと90°縮めればよいわけです。