皆様こんにちは。大木快です。
今回は、入試頻出の、半径が求められない円の面積を考えます。例によって親子が解決していきますよ。
良夫:円の面積の求め方を習ったよ。
父:ほほう。
良夫:半径✕半径✕3.14で出せるんだって。
父:じゃあ早速この問題をやってみよう!
良夫:余計なこと言わなきゃよかったな。ええっと、半径は…あれ?
半径不明なんだけど。
父:何だ、もうアウトか。
良夫:せっかく覚えた公式が使えないなんて…
父:1辺が4㎝の正方形の内側にぴったりとくっついている円がある。
この円の面積を考えてみようか。

良夫:半径は2だね。2×2×3.14だから面積は12.56かな。
父:うん。実はこの図の中に面積が2×2で表せる図形がある。わかるかな。
良夫:ええっと、この正方形がそうだね。全部で4個ある。
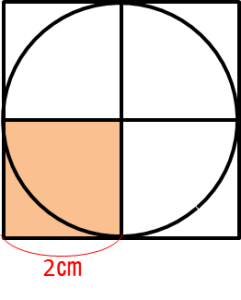
じゃあ、もう一度円の面積を求めた式2×2×3.14と比べてみると。
良夫:半径✕半径が正方形と同じだから、
円の面積は正方形✕3.14になっているんだ。
父:じゃあ例題の円は求められるんじゃないかな。さっきと同じようにまず正方形で囲ってみようか。
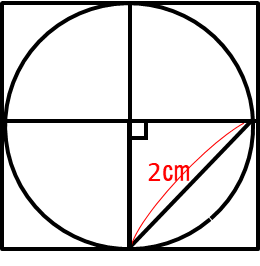
良夫:この図の小さい方の正方形の面積が分かればいいわけだね。
1辺というより、対角線が分かっていることになるなあ。
父:そう。対角線から面積は出せるかな。
良夫:だって正方形だよ。
父:正方形ってことは…ひし形でもある。
良夫:そうか、対角線✕対角線÷2が使えるんだね。
父:実は、この問題では円の半径はきれいな数として求めることはできないんだ。
良夫:分数とか?
父:いや、それすらもできない。
良夫:何と。それじゃあもし半径を求めようとしたら…
父:その瞬間に、ゲームオーバーだな。
良夫:それはひどい!それだったら最初っから
「正方形✕3.14」 て言ってくれれば迷わなくて済むんじゃないの。
父:的を射た指摘だ。
良夫:だってさ、半径×半径×3.14にとらわれると、誰だって半径を求めたくなっちゃうよ。
公式は自分を縛るものではなく、自分を解放してくれるものでなくっちゃね。
いかがでしたか。
この会話で良夫が言うように、公式はそれを活用することで、煩雑さから解放されることに一番大きな意味があります。
ただ、覚えて活用することのみに目が行くと、理解が後回しになり、結局覚える負担が大きく、定着もよくないというパターンに陥ります。
公式の成り立ちや意味を考えることは、一見無駄道のようではありますが、結果的に効率が良くなります。楽しく勉強した方が有利になるという、逆説的なお話でした。
それではまた。





