7/22(日)に自由が丘校にて
「御三家選抜プライベートレッスン(少人数授業+過去問添削)」
を開催させて頂きました。
開成・桜蔭必勝コースには非常にレベルの高い生徒様が参加してくださり、
有意義な時間をすごせたと思っております。
今回は「開成必勝コース」で扱った問題を取り上げます。
【問 題1】
(1) 5円玉と10円玉、50円玉をそれぞれ1まい以上使って120円にするには、
全部で何通りの方法がありますか。
(2) 1まいのねだんが50円、80円、120円の切手を合わせて30まい買って、
全部で2400円はらいました。3種類の切手の買い方は何通り考えられますか。
ただし、どの切手も少なくとも1まいは買うものとします。
【問 題2】
ツル、カメ、トンボの数をかぞえました。かりにツルの数をカメの数とし、カメの数をトンボの数とし、
トンボの数をツルの数とすると、足の本数の合計は200本となります。
一方、実際の足の本数の合計もやはり200本になります。
実際のツルの数として考えられるものをすべて答えなさい。
ただし、ツル、カメ、トンボの数はすべて1以上とします。
なお、ツル、カメ、トンボの足の本数はそれぞれ2本、4本、6本です。 [開成]
【解答・解説】
テキストは各単元、基本問題と開成の過去問で構成、基本問題の解法が
開成の過去問で応用できる形になっており、基本問題で基礎力をはかり、
開成の過去問で根本的な考え方の理解と応用力をみることができます。
問題1の解説はスペースの関係上、割愛して答だけ掲載します.
問題1 (1) 7通り (2) 4通り
問題2 開成の過去問にうつります。
つるかめ算のポイントは
【考え方のポイント】 ①「1つを全部と考えたらどうなるか」 がスタート
②3つのつるかめ算は2つにする
【解き方のポイント】 ①面積図で解く ②表で解く
→ 両方できるようにしておく
です。
まず、問題文の内容を理解します。
①「ツル、カメ、トンボの実際の足の本数の合計は200本」
②「ツルの数をカメの数とし、カメの数をトンボの数とし、
トンボの数をツルの数とすると足の本数の合計は200本」
です。文章を読んでも次に進めない場合は図を書いて解法の糸口を探します。
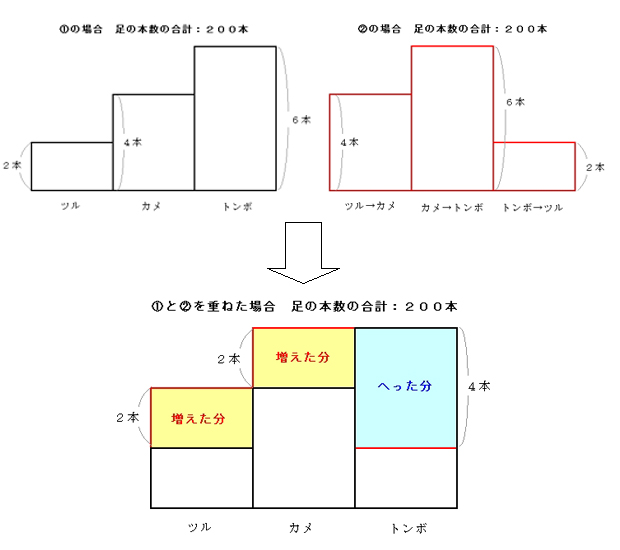
①も②も足の本数の合計は200本で同じですので、増えた分の合計と減った分の合計は
同じになります。
ツルの数×2+カメの数×2=トンボの数×4
(ツルの数+カメの数)×2=トンボの数×4
ツルの数+カメの数=トンボの数×2
この式を使って、考え方のポイント②「3つを2つ」にします。
下図のように
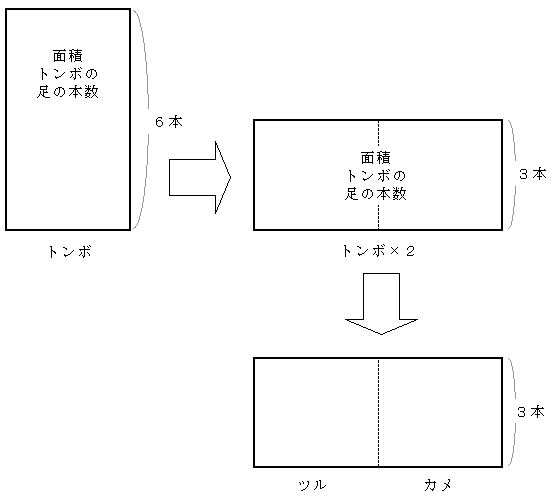
トンボの足の本数=トンボの数×6本=(トンボの数×2)×3本
とし、
トンボの数×2=ツルの数+カメの数
ですから
トンボの足の本数=(ツルの数+カメの数)×3本=ツルの数×3+カメの数×3
と置きかえることができます。
これをもとの図に置きかえ、ツルとカメだけの面積図にすると下図のようになります。
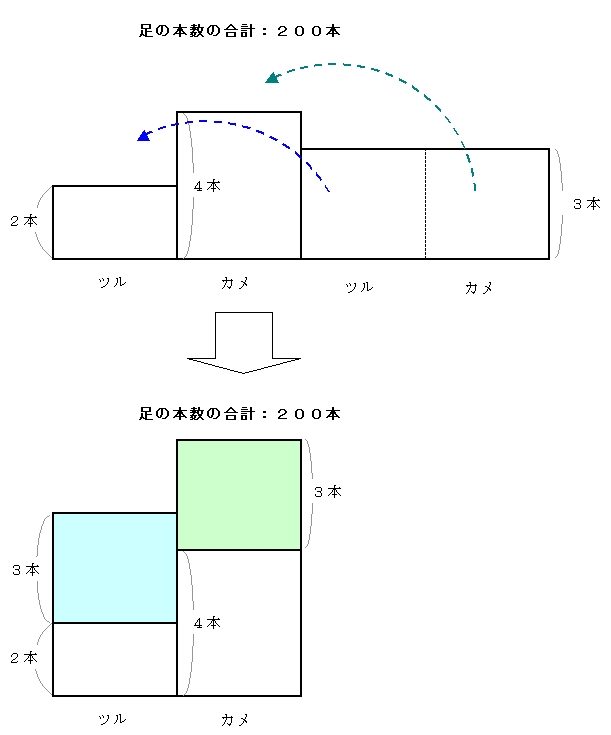
あとは表で解くだけです。

答 5、12,19、26、33
いかがでしたでしょうか。
このように開成の問題は、ひとつの解き方ではなく、基本的な複数の解き方を組み合わせて
解く問題が多いのです。
1つの問題に対して、ただ、答があっていた、というので満足することなく
ほかに解き方はないか、他の単元の解き方は応用できないか、
など、1つの問題を掘り下げ、その根本的な考え方を
きちんと理解し、難しい複雑な問題にも、基本な解き方を当てはめて解くことが
できる力を応用力といいます。
この「応用力」を身につけることが必要です。
今回の「開成必勝コース」の授業は開成の中でも比較的難易度の低い問題を扱いました。
今後とも、さらに開成の問題を解くことができる「算数の本質」に迫っていきたいと思います。
開催の際には是非ご参加を宜しくお願いします。


