みなさん、こんにちは。受験Dr.の桑田陽一です。

今回は、「中学受験生も解ける大学入試数学」シリーズの2025年度第2弾として、2月25日に行われた東京大学の入学試験を題材に、1問紹介します。

問題

白玉2個が横に並んでいます。コインを用いて次の手順をくり返し、白玉または黒玉を横一列に並べていきます。

手順
コインを投げ、表が出たら白玉、裏が出たら黒玉を、それまでに並べられている一番右にある玉の右隣におく。そして、新しくおいた玉の色がその1つ左の玉の色と異なり、かつ2つ左の玉の色と一致するときには、新しくおいた玉の1つ左の玉を新しくおいた玉と同じ色の玉に取りかえる。

例えば、手順を2回行い、コインが裏、表の順に出た場合には、白玉が4つ並びます。

(1) 手順を3回行ったとき、右から2番目の玉が白玉であるようなコインの表裏の出方は何通りですか。
(2) 手順を5回行ったとき、右から2番目の玉が白玉であるようなコインの表裏の出方は何通りですか。
(3) 手順を8回行ったとき、右から1番目と2番目の玉がともに白玉であるようなコインの表裏の出方は何通りですか。

（2025　東京大学　文科第3問　改）

東大で出題された元の問題は、中学以降で学習する「確率」の問題でした。
ここでは「場合の数」の問題に改め、中学受験生にもチャレンジできる形にしましたが、問題文の表記や本質的な内容は、なるべく変わらないようにしています。

まずは、(1)から考えてみましょう。
「手順」に記された操作のうち、「そして、」以降の理解がポイントです。
「このくらいなら出来そうだ！」と思った人、ぜひ紙を用意して取り組んでみてください。
実際、(1)は丁寧に樹形図を書いて調べれば充分ですよ！

…
…
…
…
…

では、(1)の解説。

「そして、」以降の操作はきちんと理解できましたか？
基本的には、表が出たら白玉が、裏が出たら黒玉が右端に付け加えられますね。
ただし、「新しくおいた玉の色がその1つ左の玉の色と異なり、かつ2つ左の玉の色と一致するとき」、
つまり、新しく玉をおいた結果、右端の3つが「○●○」や「●○●」のようになったときには、「新しくおいた玉の1つ左の玉を新しくおいた玉と同じ色の玉に取りかえる」。
よって、「○●○」→「○○○」と置きかえ、「●○●」→「●●●」と置きかえるということです。

このことに注意しながら、まずは樹形図を書いて様子を調べてみましょう。

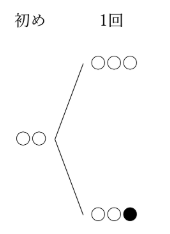
1回目の手順では、表が出ても裏が出ても、単に白玉・黒玉が付け加えられるだけですね。
しかし…

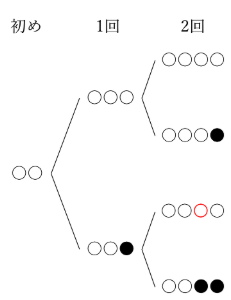
1回目で●、2回目で○が付け加えられると、●が○に置きかえられます(上の樹形図の赤い部分)。
さらにもう1回手順を行うと…。

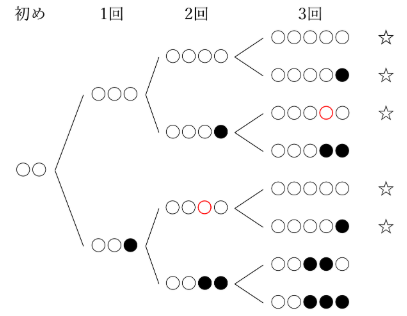
再び、●→○と置きかえられる枝が発生しています。
これにて、作業は終了。「右から2番目の玉が白玉」になっているのは、☆をつけた5通りです。

さて、この調子で(2)(3)と考えていきたいのですが、完全な樹形図を書くのはかなり大変。
そこで、「右端の2個だけ」に注目した樹形図にしてみるとどうでしょうか？

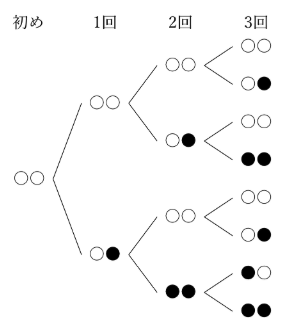
これならば、何とかなりそう？
意欲が湧いてきたら、(2)を解いてみましょう！

…
…
…
…
…

では、(2)の解説です。

何はともあれ、先ほどの「右端2個だけ」に注目した樹形図の続きを5回目まで書いてみます。

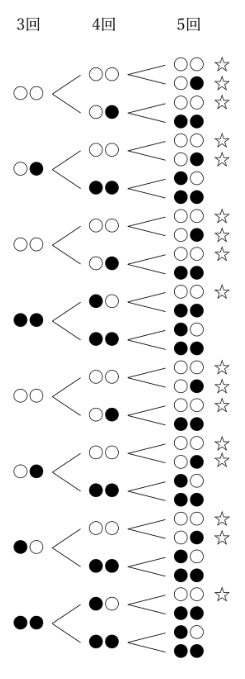
結構大変でしたが、こんな感じ。「右から2番目の玉が白玉」なのは、☆をつけた17通りです！

よし、この調子で(3)も……というのは、さすがに大変そうですね。
実際にすべて書いたとすると、2×2×2×2×2×2×2×2＝256本の枝が現れることになります。

ここで、(2)で書いた樹形図の様子を、よく観察してみると…。

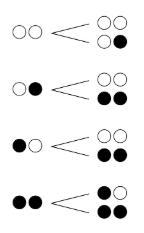
上記の4パターンの枝分かれだけが繰り返し現れていることが分かります。
また、(2)で書いた樹形図の5回目のところには、「○○」が11個、「○●」が6個、「●○」が5個、「●●」が10個あることを確認してください。
そして、上記の4パターンを考えると、6回目には「○○」「○●」「●○」「●●」がそれぞれ何個現れるか、計算できないでしょうか…？

…
…
…
…
…

「よーし、分かった！」という人もいそうですが、長くなってきたので、今回はいったんここまで。
次回は、(3)の解決編です！

今回は、ここまで。