みなさんこんにちは。
受験Dr.の久米です。

今回は前回に引き続き、算数の「集合算」についてお話しします。
前回は下のように、質問が2つの問題を表に整理する方法をお話ししました。

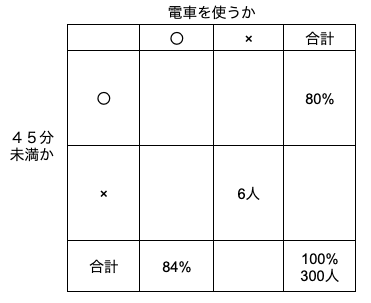
今回は質問3つの問題についてお話しします。

例題1
39人のクラスでキャベツ、ニンジン、ピーマンが好きかどうかのアンケートをとりました。
キャベツが好きな人は27人、ニンジンが好きな人は23人、ピーマンが好きな人は10人
また、キャベツとニンジンの両方が好きでない人は3人、
キャベツとピーマンの両方が好きでない人は6人でした。
また、3つ全部好きな人は1人いて、3つ全部好きでない人はいませんでした。
⑴　キャベツとニンジンの両方が好きな人は何人ですか。
⑵　ニンジンとピーマンの両方が好きな人は何人ですか。

例題1の質問は
「キャベツが好きか」「ニンジンが好きか」「ピーマンが好きか」の3種類、
答え方は「好き」「好きでない」の2種類です。
ですから、例題1は「質問が3つ、答え方が2つ」の問題といえます。
「質問Aの答え方×質問Bの答え方×質問Cの答え方＝区分する数」となるので、
「2×2×2＝8」から、全体を8つに区切った図で表すことになります。
これをベン図で表してみます。

ベン図は全体のイメージを表すことに優れています。
〇の数が質問の数で（今回は3つ）、
〇の内部にあるか外部にあるかで質問に対する答えを区分しており、
全体は㋐～㋗の8つに分かれています。

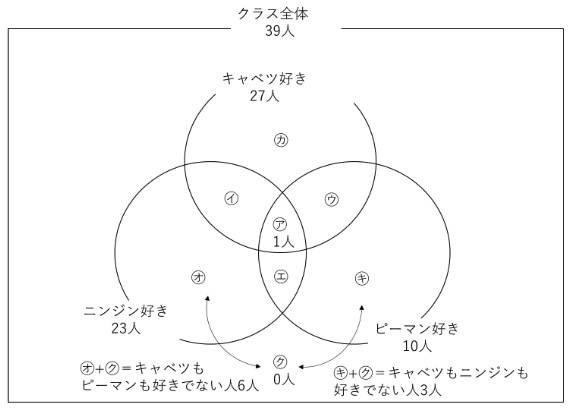
㋐はキャベツ好き、ニンジン好き、ピーマン好き
㋑はキャベツ好き、ニンジン好き、ピーマン好きでない…のように読み取ります。
「キャベツもニンジンの両方が好きでない3人」は「㋖+㋗」
「キャベツとピーマンの両方が好きでない人6人」は「㋔+㋗」となります。
〇の外側は条件に当てはまらないものになることを使って考えましょう。
㋖+㋗＝3人で㋗＝0人なので、3－０＝3人…㋖
㋔+㋗＝6人で㋗＝0人なので、6－０＝6人…㋔
このように考えていくと（式が長くなるので途中は省略します）、
⑴14人　⑵4人　となります。

例題2
ある会社では、社員200人全員がワクチンを3回接種しました。
ワクチンにはAとBの2種類があり、次の4つのことが分かっています。
・1回目にAを接種した人は110人
・1回目、2回目の両方ともAを接種した人は66人
・1回目、2回目の両方ともにBを接種した人は63人
・3回ともAを接種した人は36人で、3回ともBを接種した人より2人少ない
次の問いに答えなさい
⑴　1回目にA、2回目にBを接種した人は、1回目にB、2回目にAを接種した人より
何人少ないですか。
⑵　3回のうち、Aを2回だけ接種した人とBを2回だけ接種した人は合わせて何人ですか。

例題2は、問題の条件をどうやって区分するのかがポイントです。
質問は3つあります。
答え方はAとBの2種類あります。
したがって、例題1と同様に、「2×2×2＝8つに区分する」ということが分かります。
表整理の解法を使い、以下のように表を書きます。
横を4つ、たてを2つに分けて見やすくすることがポイントです。

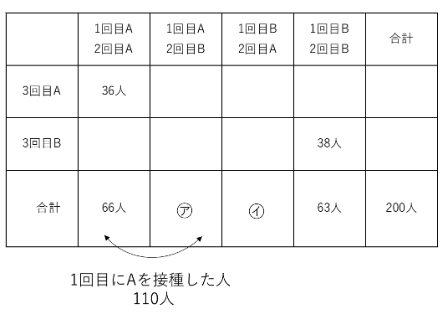
⑴　1回目にA、2回目にBを接種した人は図の㋐なので110－66＝44人
1回目にB、2回目にAを接種した人は図の㋑なので200－（110＋63）＝27人
㋐－㋑＝44－27＝17人

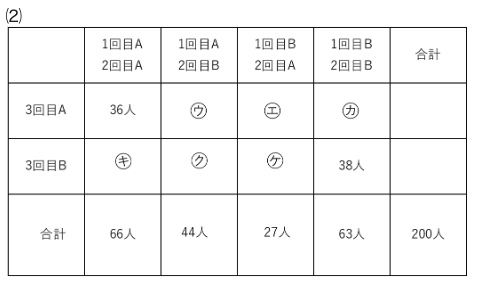
Aを2回だけ接種した人は図の㋒+㋓+㋖
Bを2回だけ接種した人は図の㋕+㋗+㋘なので、
全体200人から、Aを3回接種した人とBを3回接種した人を引けば答えが出ます。
200－（36＋38）＝126人

例題1と同様に、ベン図で表すこともできます。

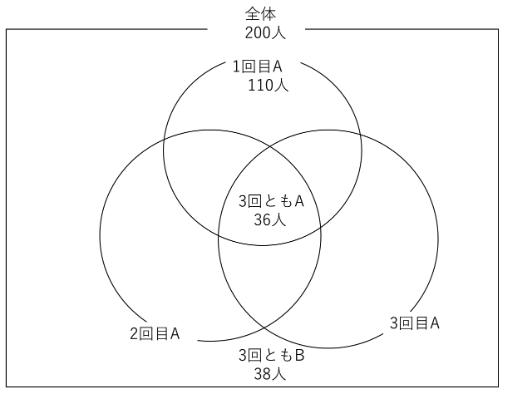
ただしこの問題については、ベン図のどこが何をあらわすのか見づらいので、
表整理の方が分かりやすいと思います。

このような発展的な集合算では、全体をいくつに区分するのかを考えて解きましょう。

それではまた。
受験Dr.、久米でした。