みなさん、こんにちは。
受験ドクター算数・理科科の川上と申します。

先日、ちょっと変わった問題を見つけたので紹介いたします。

［解説］

そもそも、どんな規則なのかを捉えるのもやや難しく、どこから手をつけようか迷うような問題です。

塾によっては、最近「N進法」を学習したのではないでしょうか。

「1、5、25、125、625」を見て、5進法と関りがあるのではないか、と考えを巡らせることができれば、この問題の本質に大きく近づくことができます。

与えられた数列を、5進法に変換します。

念のため、10進法の数を5進法に変換する方法を確認しておきます。変換に問題が無ければここは読み飛ばしていただいて構いません。

（例）10進法の423を5進法に直す

以下の図のように、423を5で割ります。

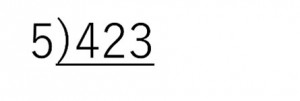
商を下に、あまりを右に記入していきます。

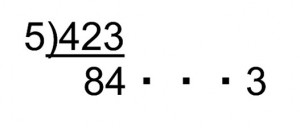
これを、商が5より小さくなるまで行ったのが下の図です。

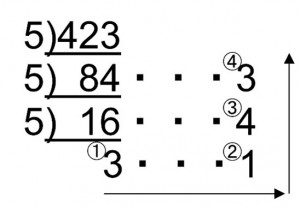
この商とあまりを①②③④の順に読み上げて出来た「3143」が答えとなります。

また、5進法の3143を10進法にすると423に戻るかどうかも確認しておきましょう。

（例）5進法の3143を10進法に直す

5進法だと、各位は右から順に「1の位」「5の位」「25の位」「125の位」となります。

よって、5進法の3143は10進法に変換すると

125×3＋25×1＋5×4＋1×3＝423となります。
確かに元の423に戻りましたね。

さて、本題に戻ります。もとの数列を5進法に変換します。

［元の数列］
1,5,6,25,26,30,31,125,126,130,131,150,・・・

［5進法に直したもの］
1,10,11,100,101,110,111,1000,1001,1010,1011,1100,・・・

5進法に変換したにもかかわらず、0と1しか使われていない、2進法のような表記になりました。しかも小さい順に並んでいます。

2進法の30番目は11110となりますが、実際のこの数値は5進法になるので

625×1＋125×1＋25×1＋5×1＝780

となります。

ちなみにこの数列にある数字は

6＝1＋5
26＝1＋25
31＝1＋5＋25

のように、1、5、25、125、625、・・・のそれぞれの数字を使うか、使わないか選び、和を取ることで作られています。
ここに気付くことができれば、別の解法もありそうですね。

数の性質の問題では、このようにN進法に帰着させることで劇的に考えやすくなるものもあります。ご参考になれば幸いです。

それでは、失礼いたします。

受験ドクター　川上亮