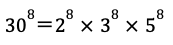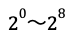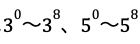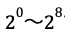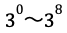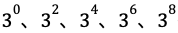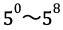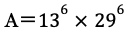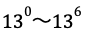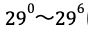みなさん、こんにちは。
受験ドクター算数・理科科の川上と申します。

本日はタイトルの通り、余りに関する問題について触れたいと思います。
一口に「余りに関する問題」と言っても沢山ありますが、「本日は割り算のあまりの積の利用」をテーマに話を進めていきます。

まずは例題です。

【例題】

1001を6で割った余りを求めなさい。

【解説】

もちろんそのまま計算しても構いませんが、せっかくですので工夫して解き進めていきましょう。

1001＝7×11×13

と素因数分解できます。

7、11、13をそれぞれ6で割ってみます。

7÷6＝1余り1
11÷6＝1余り5
13÷6＝2余り1

です。

答えはそれぞれの余りを掛け合わせた、1×5×1＝5となります。

この考え方が破壊力抜群で、特に灘中入試において必須と言える考え方です。

【問題】
30を8個かけてできる数30×30×30×30×30×30×30×30の約数のうち、4で割ると1余るものは全部で何個ありますか。(2018　灘中　1日目　抜粋)

【解説】

30＝2×3×5ですので、30を8回掛け合わせた数は、2を8回掛け合わせた数と、3を8回掛け合わせた数と、5を8回掛け合わせた数の積となります。

さて、約数の個数についての問題でも学習したかもしれませんが、
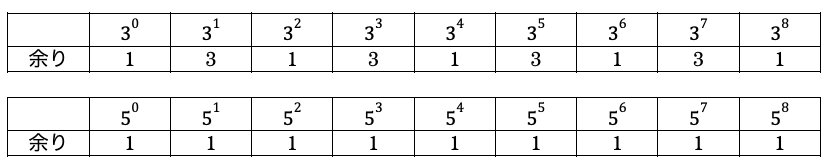
Aがどんな数字であろうとなります。

について、4で割った余りを考えます。

同様にについてもまとめます。

余りを1にするためには、それぞれの余りの積を1にする必要があります。

ではの1通り
ではの5通り
ではの9通り

よって、1×5×9＝45個が答えとなります。

2019年度入試においても、類似の問題が出題されました。

【問題】A＝377×377×377×377×377×377とするとき、Aの約数の中で14で割ると1余るものは、1を含めて何個ありますか。また、Aの約数の中で15で割ると1余るものは、1を含めて全部で何個ありますか。(2019　灘中　1日目)

【解説】

377＝13×29

と、素因数分解できます。

よって

について、14で割った余りを考えます。

についても同様にまとめます。

答えは4×7＝28となります。

15で割ると1余る数についても同様に考えれば簡単に解くことができます。
是非チャレンジしてみてください。

ちなみに、本日の内容は数学で「合同式」と呼ばれる等式の考え方となります。
難しい内容でしたが、使いこなせるよう練習してみてください。

それでは、今回はこれで失礼します。

受験ドクター　川上亮