みなさん、こんにちは。受験ドクターの亀井章三です。
今回も立体図形より「影の問題」です。
前回お伝えした内容は、点の位置をXYZ座標で捉えるという解法でした。
詳しくは前回のブログをご参照ください。
今回は応用編ということで、開成中の問題をこの解法を使って解いていきたいと思います。
まずは次の問題をご覧ください。
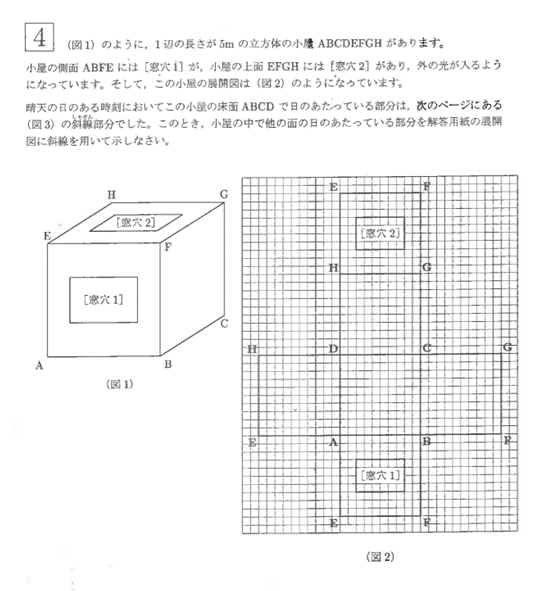
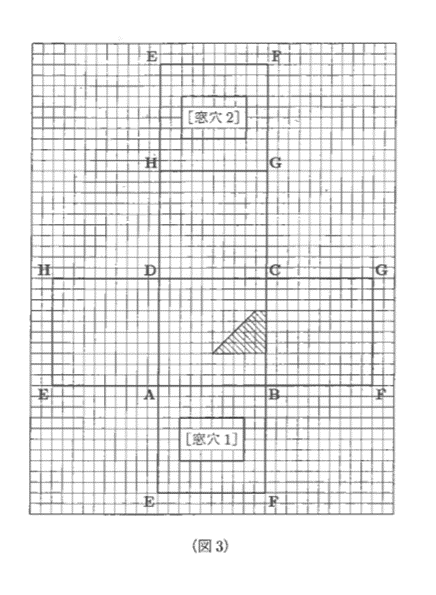
(開成中 2020入試問題より)
まず、立方体Aを基準として下の図のように線を3本引きます。
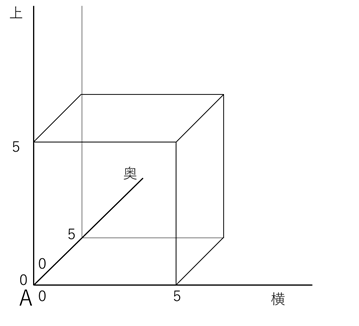
そして、立方体の頂点や辺、面の上にある点の位置を、
(Aから何m横か、Aから何m奥か、Aから何m上か)で表すことにします。
例えば、B~Hの位置は
B( 5 , 0 , 0 ) C( 5 , 5 , 0 ) D( 0 , 5 , 0 )
E( 0 , 0 , 5 ) F( 5 , 0 , 5 ) G( 5 , 5 , 5 ) H( 0 , 5 , 5 )
と表せます。
① 光の射しこむ方向を求める
今、面ABCD上に台形の光が当たっています。これが窓穴2から入った光だとすると、窓穴の縦の辺はEHに平行なのに、床の光の左端の線はEHと平行ではないため、おかしいことになります。
よって、床の光は窓穴1から入ったものとわかります。
窓穴1の4隅の点をI、J、K、L、床の光の2点をM、Nとします。
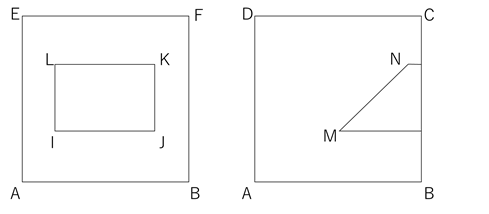
窓穴よりも床の光が右側に来ていますので、光は窓穴1より左の方向から射しています。
よって、MはIを通った光、NはLを通った光と考えられます。
Iの位置は( 1 , 0 , 1.5 ) Mの位置は( 2.5 , 1.5 , 0 )
ここから、光の射し方は、
「横に1.5m進むと、奥にも1.5m進み、下に1.5m下がる」
と求められます。それぞれの長さは比例しますので、
「横に〇m進むと、奥にも〇m進み、下に〇m下がる」のが光の道筋です。
これをL→Nで確かめます。
Lの位置は( 1 , 0 , 3.5 ) Nの位置は( 4.5 , 3.5 , 0 )であり、
確かに「横に3.5m進むと、奥にも3.5m進み、下に3.5m下がる」となっています。
② 窓穴1から入った光が、側面に当たる部分を求める
光の道筋が分かったので、残りの頂点J、Kを通った光を考えます。
Jの位置は( 4 , 0 , 1.5 )です。この光は、側面BCGFに当たります。
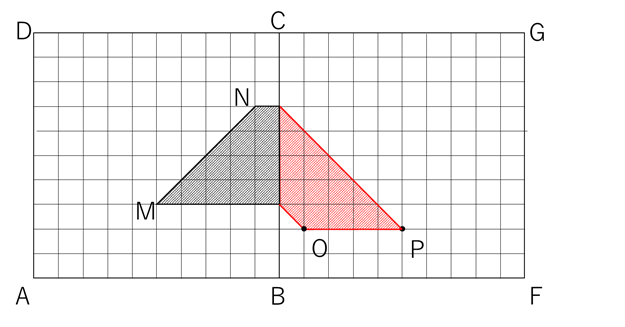
Jを通った光が側面BCGFに当たる点をOとします。
側面BCGFはAから横に5mのところにあるため、Oの位置は( 5 , ? , ? )となります。
するとJからOは横に1m進んだので、奥にも1m進み、下に1m下がることになります。
そこからOの位置は、( 4+1 , 0+1 , 1.5-1 )=( 5 , 1 , 0.5 )となります。
同様に、Kを通った光が側面BCGFに当たる点をPとすると、
Kの位置は( 4 , 0 , 3.5 )、Pの位置は( 5 , ? , ? )で1m動いていますので、
Pの位置は( 4+1 , 0+1 , 3.5-1 )=( 5 , 1 , 2.5 )となります。
この2点を解答用紙の図に加えます。
窓枠1の辺はそれぞれ、IJ→MO、JK→OP、KL→PN、LI→NMとなります。
MからOに向かう直線は、辺BCのところで折れ曲がることに注意しましょう。
③ 窓穴2から入った光が、側面に当たる部分を求める
ここまで来ればもう少しです。光の道筋は同じなので、同じ作業を行います。
窓穴2の4隅の点をQ、R、S、T、それぞれが側面に当たる点をU、V、W、Xとします。
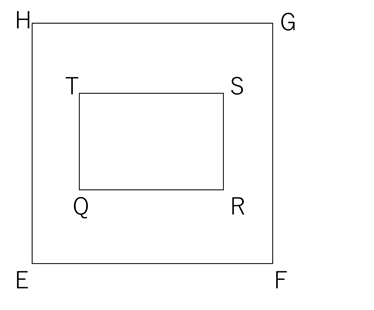
Q、R、S、Tの位置はそれぞれ
Q( 1 , 1.5 , 5 ) R( 4 , 1.5 , 5 ) S( 4 , 3.5 , 5 ) T( 1 , 3.5 , 5 ) です。
窓穴2から入った光は、側面CDHGか側面BCGFに当たります。
側面CDHGにある点は全て、( ? , 5 , ? )と表すことができ、
側面BCFGにある点は全て、( 5 , ? , ? )と表すことができます。
まず、側面CDHGに当たるかどうか考えます。
Q→UのUがCDHGにあるとすると、( 1 , 1.5 , 5 )→( ? , 5 , ? )より
3.5m奥に移動したことになります。
そうするとUの位置は、( 1+3.5 , 1.5+3.5 , 5-3.5 )=( 4.5 , 5 , 1.5 )になりCDHG上にあることがわかります。
R→Vの場合 ( 4 , 1.5 , 5 )→( ? , 5 , ? ) 奥に3.5m移動
Vの位置は、( 4+3.5 , 1.5+3.5 , 5-3.5 )=( 7.5 , 5 , 1.5 )となり、これは立方体の1辺5mを超えてしまいます。つまり、Rを通った光は側面CDHGには当たらないということです。
S→Wの場合 ( 4 , 3.5 , 5 )→( ? , 5 , ? ) 奥に1.5m移動
Wの位置は、( 4+1.5 , 3.5+1.5 , 5-1.5 )=( 5.5 , 5 , 3.5 )となり、これもCDHGにはないことになります。
T→Xの場合 ( 1 , 3.5 , 5 )→( ? , 5 , ? ) 奥に1.5m移動
Xの位置は、( 1+1.5 , 3.5+1.5 , 5-1.5 )=( 2.5 , 5 , 3.5 )になりCDHG上にあります。
CDHGに点がないVとWはBCFG上にあることになります。
R→Vの場合 ( 4 , 1.5 , 5 )→( 5 , ? , ? ) 横に1m移動
Vの位置は、( 4+1 , 1.5+1 , 5-1 )=( 5 , 2.5 , 4 )になります。
S→Wの場合 ( 4 , 3.5 , 5 )→( 5 , ? , ? ) 横に1m移動
Wの位置は、( 4+1 , 3.5+1 , 5-1 )=( 5 , 4.5 , 4 )になります。
このU、V、W、Xを展開図に取り、UV、VW、WX、XUを結びます。
その時、一旦下の図のように、CDHGとBCGFをくっつけて作図するとわかりやすくなります。
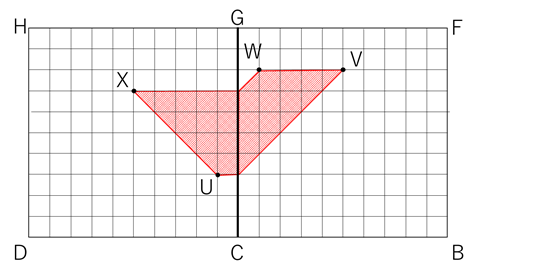
この斜線部分を解答用紙の図に書き込めば答えとなります。
かなり難しい問題でしたね。投影図を使いどの位置を光が通るか考えても解くことができますが、今回紹介した座標軸を使うと、規則がわかりやすく解きやすいものと思われます。
開成中学を目指すお子様は、他の受験生に差をつける解法としてぜひ練習してみてください。
解答は以下の図です。
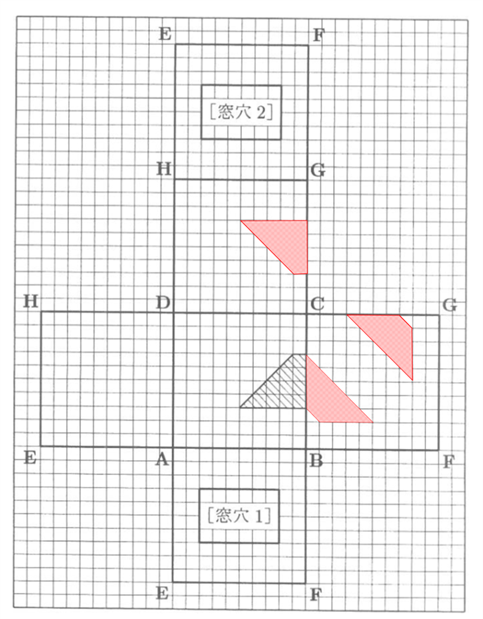
2月1日まであとわずか。頑張れ受験生!




