みなさんこんにちは。受験ドクターの石田新一です。

私たちは日頃、三次元の中で暮らしていますが、お子様が勉強するのは二次元のノートやプリントの紙面上です。二次元の紙の上に三次元の立体が描かれていて、その状態を把握し、問題を解いているということになります。
「空間把握能力」とでも申しましょうか、この能力は持って生まれた部分と、トレーニングによって得られる部分があると思います。

立体を切断すると、切断面が現れます。直線は、通る２点が決まれば一つに定まりますが、
平面を一つに定めるには、同一平面上にない３点を決めることが必要です。
入試で頻出の立体図形の問題をしっかりと得点に結びつけるために、
立体切断３つのポイントをお伝えしたいと思います。

＜ポイント其の１＞　同一平面上の点を直線で結ぶ
＜ポイント其の２＞　平行な面には平行な切断線ができる（平行な面には、相似または合同な図形ができる）
＜ポイント其の３＞　平面を拡げて切断線を延長する

（例題１）下の図は、立方体です。点M、点N、点Gを通る平面でこの立方体を切断したときの切り口の形を答えなさい。ただし、点M、点Nはそれぞれ辺CD、辺ADの真ん中の点です。

手順１　点Mと点N、点Mと点Gはそれぞれ同一平面上の点なので直線で結びます。

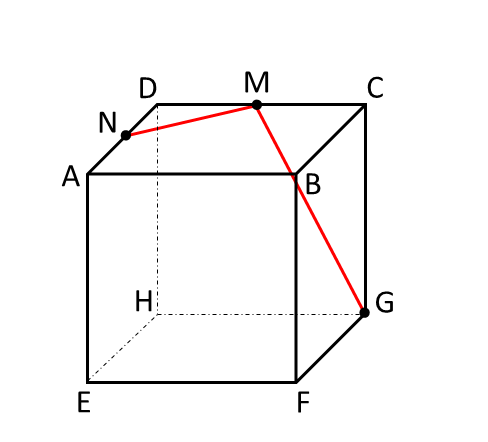
手順２　面ABCDと面EFGHは平行な面なので、点GからMNに平行な直線を引きます。
面ABCD上には直角二等辺三角形DMNができているので、面EFGHにも同様に直角二等辺三角形ができ、点GからMNに平行に引いた直線は点Eを通ります。
三角形EFGは直角二等辺三角形となっています。

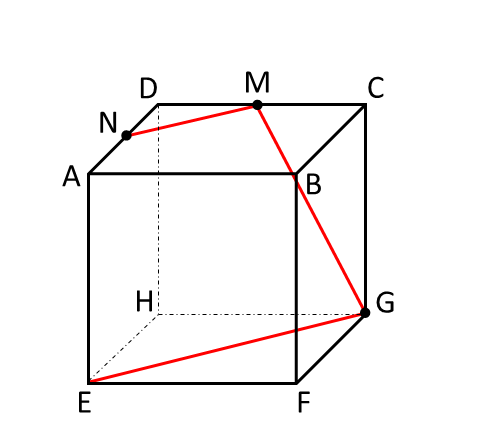
手順３　点Nと点Eは同一平面上の点になるので、この２点を直線で結びます。
これで切断面が完成です。MNとEGは平行で、MGとNEの長さは等しいので切断面の図形は「等脚台形」となります。

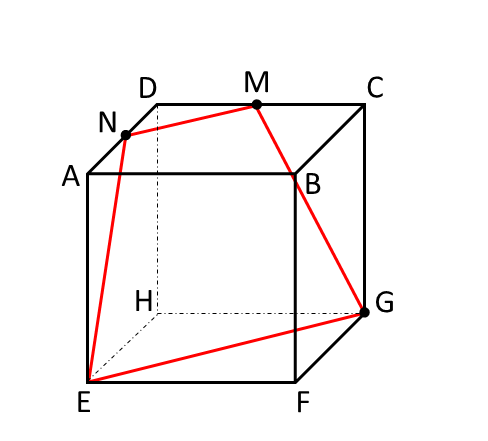
次に、＜ポイント其の３＞を利用する例題をご紹介します。

（例題２）下の図は、立方体です。点L、点M、点Nを通る平面でこの立方体を切断したときの切り口の形を答えなさい。ただし、点L、点M、点Nはそれぞれ辺EF、辺CD、辺ADの真ん中の点です。

手順１　点Mと点Nは同一平面上の点なので直線で結びます。

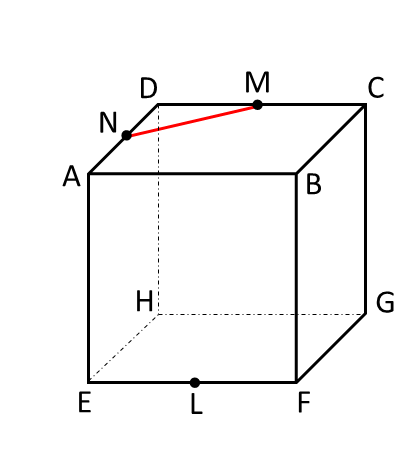
手順２　面ABCDと面EFGHは平行な面なので、点LからMNに平行な直線を引きます。
面ABCD上には直角二等辺三角形DMNができているので、面EFGHにも同様に直角三角形ができます。
点LからMNに平行に引いた直線は辺FGの真ん中の点Kを通ります。
三角形LFKは三角形DMNと合同な直角二等辺三角形となっています。

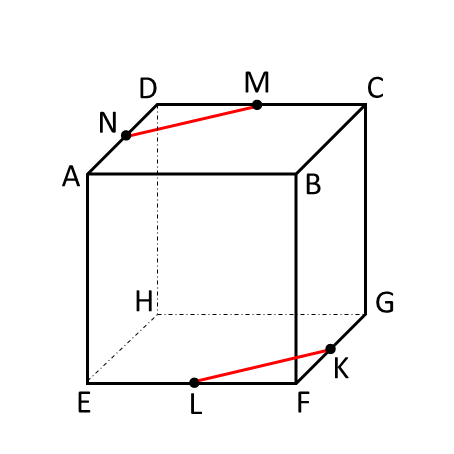
手順３　ここで＜ポイント其の３＞を使います。辺BAと辺BCをそれぞれ点A、点Cの方向に延長し、MNを左右に延長します。それぞれの交点をS、Tとします。

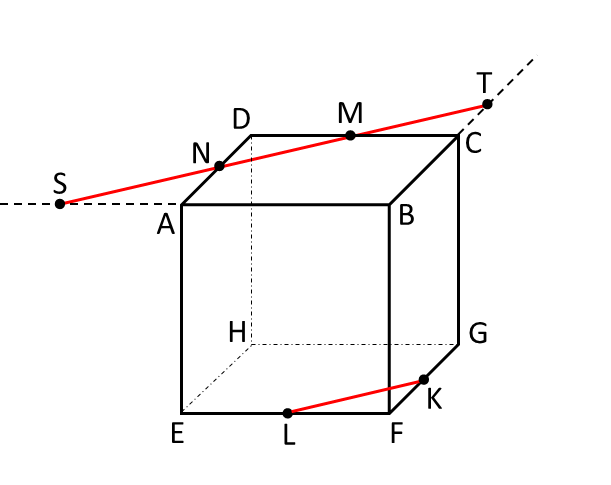
手順４　点Sと点L、点Tと点Kはそれぞれ同一平面上の点になるので直線で結びます。SLと辺AE、TKと辺CGの交点をそれぞれU、Vとします。

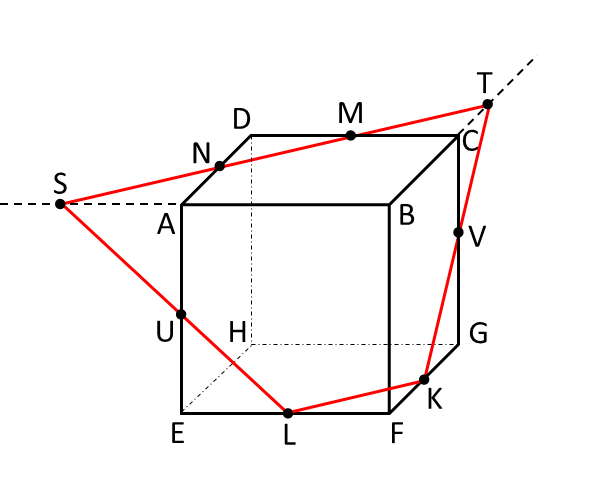
手順５　点Nと点U、点Mと点Vはそれぞれ同一平面上の点になるので直線で結びます。　立方体の面上にできた６本の切断線の長さは全て等しいので、切断面の図形は正六角形MNULKVとなります。

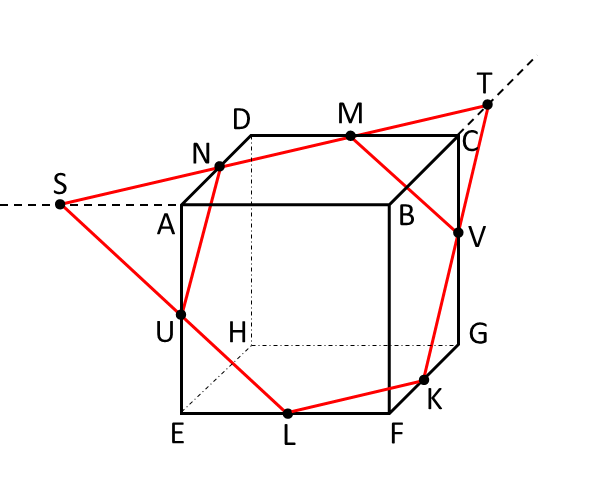
今回お伝えしました３つのポイントを使い、いろいろと立体の切断を試してみて頂ければと思います。