みなさんこんにちは。受験ドクターの石田新一です。

人間の脳は、目で見たものを信じるようにできていると思いませんか？

今回は図形の問題を目で見て分かるように解くためのポイントについてお伝えしたいと思います。

ポイントその１：わかっていることを図に書き込む！

当たり前だ！と思われるかもしれませんが、この当たり前のことが意外とできていません。

例題　下の図は、ひし形ABCDと正三角形CDEを組み合わせた図形です。
角CBDの大きさは50度です。角AEDと角BAEの大きさは、それぞれ何度ですか。

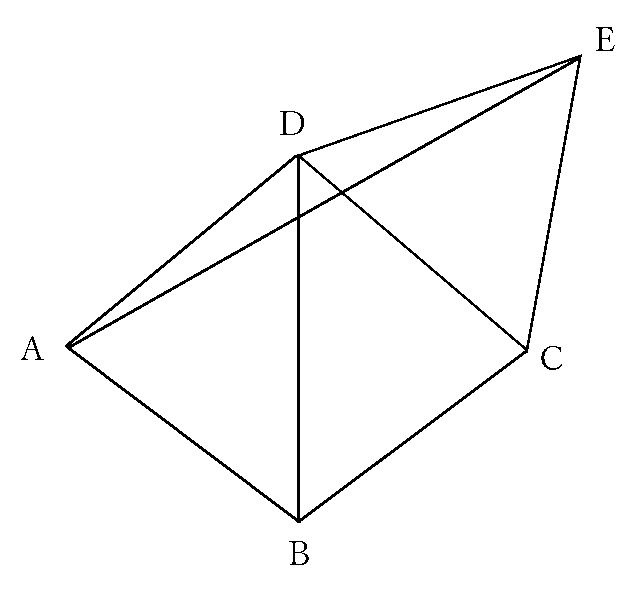
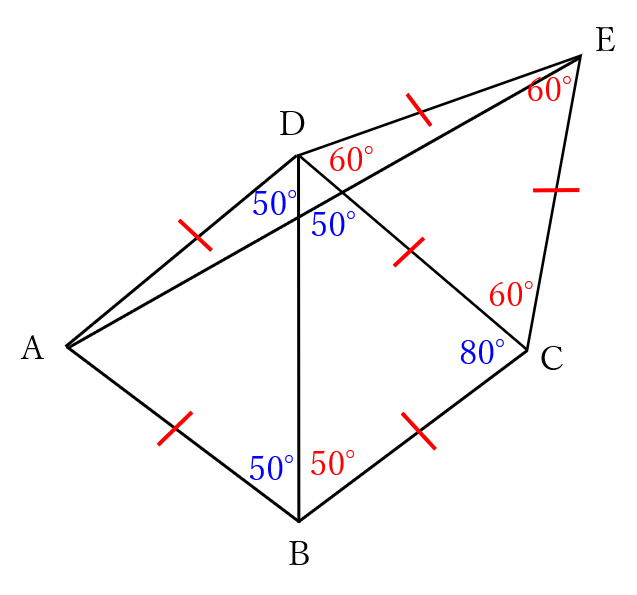
【手順１】わかっている角度、同じ長さの辺に同じ記号を書き込む

【手順２】さらにわかったことを図に書き込む

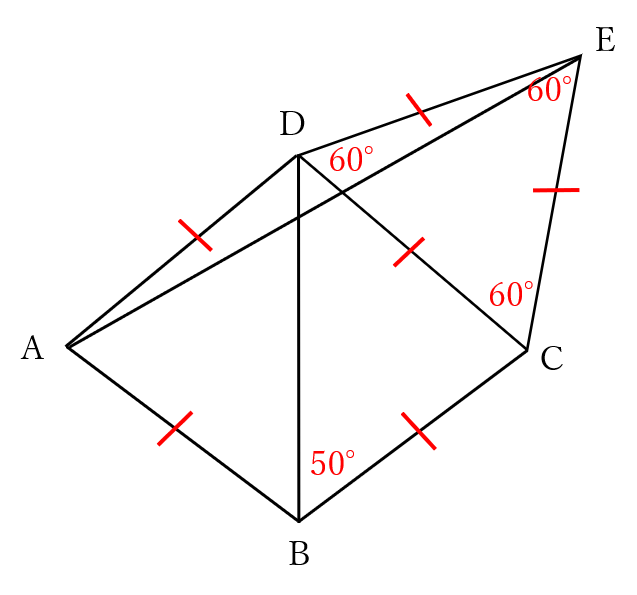
【手順３】条件を整理して、答えを導く

この問題の場合は、三角形ADEがDA＝DEの二等辺三角形になります。
よって、角AEDと角EADは等しいので、角AED＝角EAD＝(180°－160°)÷2＝10°です。
また、角BAD＝角BCD＝80°より、角BAE＝角BAD－角EAD＝80°－10°＝70°となります。

ポイントその２：補助線を引く！

補助線を１本引くだけで、景色がガラリと変わる問題が数多くあります。

例題　下の図において、xとyの値はそれぞれいくつですか。

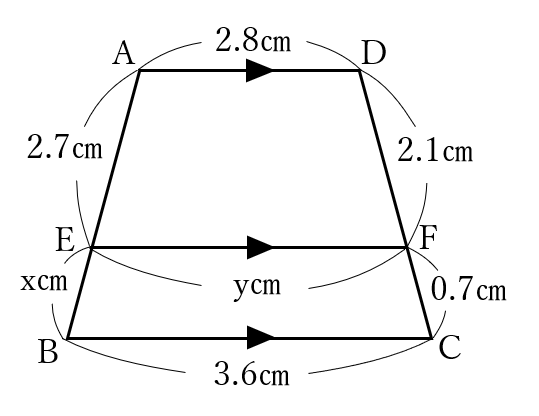
AE：EB＝DF：FC＝2.1：0.7＝3：1　より、EB＝AE×1/3＝2.7×1/3＝0.9、よってx＝0.9です。
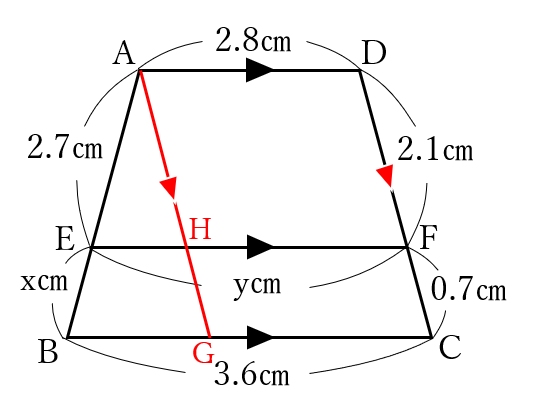
次に、下の図のように、頂点AからDCに平行な直線を引き、BCとの交点をG、EFとの交点をHとします。

四角形ADFHと四角形ADCGは平行四辺形になるので、AD＝HF＝GC＝2.8㎝です。
また、三角形AEHと三角形ABGは相似で、相似比はAH：AG＝DF：DC＝2.1：2.8＝3：4より、
EH＝BG×、BG＝BC－GC＝3.6－2.8＝0.8、よってEH＝0.8×＝0.6㎝となります。

求めたいｙは線分EFの長さなので、EF＝EH＋HF＝2.8＋0.6＝3.4 となります。

答えを求めるために書いた補助線は１本だけです！

ポイントその３：へんてこりんな形は、へんてこりんじゃない形で考える！

ポイント其の２の「補助線を引く」も使いますが、具体的な手法は次のような考え方を使います。

①図形を分けて考える
②等積変形、等積移動を利用する
③共通部分を付け足す
④部分的にではなく、全体的に図を捉える
⑤・・・

上記のように色々とありますが、問題によって使い分ける必要があります。

例題　図のように、長方形ABCDを頂点Cを中心として右回りに90°回転させました。
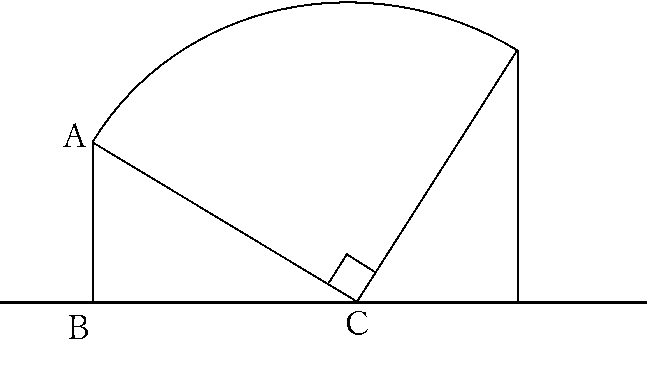
このとき、影をつけた部分（辺ABが通った部分）の面積を求めなさい。ただし、AB＝6㎝、BC＝8㎝、
長方形ABCDの対角線の長さは10㎝、円周率を3.14とします。

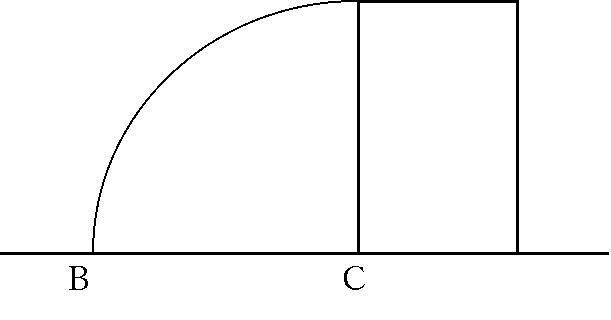
下の図のように、図形全体を2つの直角三角形と半径が長方形の対角線、中心が90°のおうぎ形として捉えます。

次に全体から取り除くべき部分は下の図のように、半径がBC、中心角が90°のおうぎ形と、長方形ABCDとなります。

全体から、いらない部分を引くわけですが、2つの直角三角形は長方形ABCDと同じですから、
答えを求める式は、10×10×3.14÷4－8×8×3.14÷4 となります。

ここで、計算の工夫をしましょう！
(10×10－8×8)×3.14÷4＝(100－64)÷4×3.14＝36÷4×3.14＝9×3.14＝28.26
よって、答えは28.26㎠ となります。

図形の問題を解く際には、他にも注意するべきポイントはありますが、とくに今回お伝えしました
３つのポイントが最重要だと思います。
これから図形の問題を解くときは、以上のポイントを意識してみてください！

次回は、「立体の切断のポイント」についてお伝えしようと思います。乞うご期待！！