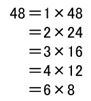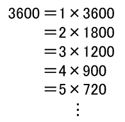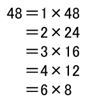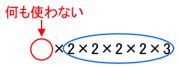みなさん、こんにちは。
受験ドクター算数科の江田です。

10月もあと10日。
1月校の受験を控えている6年生は、
入試本番まで100日を切って気が引き締まっていることでしょう。

体調管理には十分気を付けて
頑張ってくださいね♪

さて、
前回・前々回と、
「支払うことのできる金額」
というものをテーマにお話をしました。

今回のブログでは
次のような問題についてお話したいと思います。
さっそく問題です！（超シンプルな問題です。）

【問題1】
48の約数は何個ありますか。

以上。

制限時間は1分です。
どうぞ！

（考え中）

答え、出ましたか？

48を2つの整数の積のかたちで表していけば約数が見つかりますね。
実際に書き出してみましょうか。

となりますので、約数は
1，2，3，4，6，8，12，16，24，48
の10個あることがわかります。

では、次の問題はどうでしょう。

【問題2】
3600の約数は何個ありますか。

以上。
制限時間は先ほどと同じく1分にしましょうか。
どうぞ！

（考え中）

さて、
答えは出ましたか？

先ほどと同じく
2つの整数の積のかたちで表していきましょうか。

うぅ…
多くね！？
めんどくさっ！
時間が足りない！

となりませんか？
しかも、1つ1つ組み合わせを探していく中で、
「すべての組み合わせを抜けがないように書き出す」
ことは結構難しいのではないでしょうか。

当然
1セットでも組み合わせが抜けてしまったら
個数は合わなくなってしまいますからね。

では、どのように正確に求めればよいのでしょう。

【問題1】 を例にとって見てみます。
48の約数を考える際に

というように、組み合わせをすべて書き出していきました。

これらの組み合わせを次のようにとらえてみましょう。

まず、48を素因数分解します。
すなわち、素数だけの積のかたちで表します。
すると、

48＝2×2×2×2×3

となりますね。

ここで、

のように、赤のかたまりと青のかたまりに分けてみると
(2×2)×(2×2×3)＝4×12
という組み合わせを考えたことになります。

他にも

のように分けると
(2×2×2)×(2×3)＝8×6
という組み合わせを考えたことになります。
この場合の
8×6
の「8」は、
素因数分解して現れた 「“2”を3個使ってできる数」
であり、「6」は、
素因数分解して現れた 「“2”を1個、“3”を1個使ってできる数」
であることがわかりますね。

つまり、
48の約数というのは
素因数分解して現れた“2”を何個使うか、また、“3”を何個使うか
によって決まる数であると言えます。

ですから、
この考え方が全部で何通りあるのかを考えれば、
約数が全部で何個あるのかがわかる
わけです。

48＝2×2×2×2×3
素因数分解すると、
“2”が4個、“3”が1個
現れました。

このうち、
“2”を何個使うか、の考え方は何通りありますか？
また、
“3”を何個使うか、の考え方は何通りありますか？

ほら、
前回・前々回にお話した
「支払うことのできる金額」
とのつながりが見えてきませんか？

100円玉を何枚使うか。
50円玉を何枚使うか。
10円玉を何枚使うか。
それらの考え方を組み合わせて
「支払うことのできる金額」を考えていきましたよね。

それと同じです！

素因数分解した中にある
“2”を何個使うか、の考え方は…
➀ 1個使う
② 2個使う
③ 3個使う
④ 4個使う
⑤ 使わない
の5通りあり、
“3”を何個使うか、の考え方は…
➀ 1個使う
②　使わない
の2通りあるので、
これらの組み合わせ方は
5×2＝10 (通り)
と求まります。

ところで、この中には
“2”も使わないし“3”も使わない
という組み合わせが含まれていますね。
この、「素因数分解して表れた数を何も使わない」という場合、

上の図のような
(1)×(2×2×2×2×3)＝1×48
の組み合わせを考えたことになり、
「1」という約数を考えたことになります。

つまり、前回の「支払うことのできる金額」とは異なり、
この「何も使わない」という1通りも約数の個数には含まれるため、
「－1」をする必要はないことがわかります。

よってそのまま10通り　→　10個
と計算で求められるのです。

ということで、
【問題2】は…

3600を素因数分解して

3600＝2×2×2×2×3×3×5×5

となり、
“2”が4個
“3”が2個
“5”が2個
現れますので、それぞれ何個使うかを考えましょう。
“2”を何個使うか、の考え方は「使わない」も含めれば
4＋1＝5 (通り)。
同じように
“3”を何個使うか、の考え方は「使わない」も含めれば
2＋1＝3 (通り)。
“5”を何個使うか、の考え方は「使わない」も含めれば
2＋1＝3 (通り)
ですので、答えは
5×3×3＝45 (個)
と求まります。

いかがでしたか？

もちろん、受験生であればこの
「約数の個数を計算で求める方法」
は必ず身につけておかなければいけないことなのですが、
考え方の基本＝根本原理
がしっかりと理解できていれば、
前回・前々回と触れたような
“一見別の問題に見えるようなもの”
でも、つながりをもって見ることができるようになると思います。

ぜひ、今後の学習においても
このような “根本原理”の理解を大切にしていってもらいたいと思います♪

それではまた次回お会いしましょう！